


Next: Soluzioni proposte
Previous: Esercitazioni di Geometria I 1998/99
Geometria 1
Primo appello, sessione autunnale, 1998/99
9 settembre 1999
Esercizio 1
Siano dati in
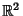
i punti
P=(0,1),
Q=(0,0) e le rette
L di equazione
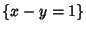
e
M di equazione
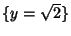
.
Si dimostri che
d(
P,
L)=
d(
Q,
M). Si costruisca un'isometria
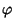
tale che
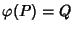
e
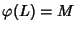
e se ne discuta l'unicità.
Soluzione
Esercizio 2
Sia
r la retta in
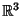
di equazioni
Si determini un vettore direzione di
r.
Fra i piani contenenti la retta
r si trovi, se esiste:
1) un piano passante per P=(1,3,1);
2) un piano parallelo alla retta
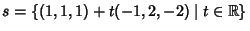 ;
;
3) un piano perpendicolare alla retta s.
Si discuta l'unicità dei piani trovati.
Soluzione
Esercizio 3
Siano dati i quattro punti
Si determini il fascio delle coniche per
P1,
P2,
P3 e
P4. Si dica se nel
fascio ci sono delle parabole e in tal caso quali sono. Si dica se nel fascio
ci sono delle circonferenze e in tal caso quali sono.
Soluzione
Esercizio 4
Sia
V lo spazio vettoriale dei polinomi in una variabile di grado minore o
uguale a
2. Si consideri il prodotto scalare definito da
Si dimostri che è non degenere, e si trovi una base ortogonale di
Vrispetto a tale prodotto.
Soluzione
Esercizio 5
Sia
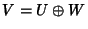
uno spazio vettoriale con un prodotto scalare
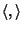
.
Supponiamo inoltre di sapere che, per ogni
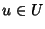
e
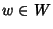
,
si ha
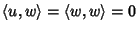
e che
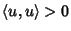
se
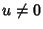
.
(i) Si dimostri che
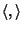 su V è semidefinito positivo.
su V è semidefinito positivo.
(ii) Si dimostri che se
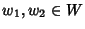 allora
allora
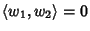 .
Suggerimento: si consideri
.
Suggerimento: si consideri
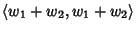 .
.
(iii) Si dimostri che
Soluzione



Next: Soluzioni proposte
Previous: Esercitazioni di Geometria I 1998/99
Domenico Luminati
1999-10-29
![]() ;
;
![]() su V è semidefinito positivo.
su V è semidefinito positivo.
![]() allora
allora
![]() .
Suggerimento: si consideri
.
Suggerimento: si consideri
![]() .
.