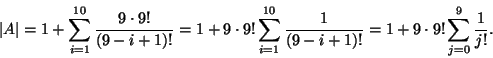Quindi la soluzione generale dell'equazione è:
Imponendo le condizioni iniziali si ottiene il sistema lineare:
Soluzione dell'esercizio 2 ![]() . Infatti
. Infatti ![]() per ogni
per ogni ![]() .
.
![]() . Infatti, dato
. Infatti, dato
![]() si ha
si ha
![]() . Infatti, se
. Infatti, se ![]() allora, dato che
allora, dato che
![]() si ha che
si ha che ![]() , ma allora, moltiplicando a sinistra e destra
per
, ma allora, moltiplicando a sinistra e destra
per ![]() entrambi i memmbri si ottiene
entrambi i memmbri si ottiene
![]() . Per
l'arbitrarietà di
. Per
l'arbitrarietà di ![]() si conclude.
si conclude.
![]() è normale. Proviamo che per ogni
è normale. Proviamo che per ogni ![]() ,
, ![]() si ha che
si ha che
![]() . Infatti
. Infatti
![]() .
.
![]() .
.
Soluzione dell'esercizio 3 Proviamo che ![]() è un sottoreticolo di
è un sottoreticolo di ![]() . Basta provare che dati
. Basta provare che dati
![]() allora
allora ![]() e
e ![]() .
.
![]() è un'algebra di Boole. Dato che le operazioni di reticolo
sono
è un'algebra di Boole. Dato che le operazioni di reticolo
sono ![]() e
e ![]() allora la relazione d'ordine è l'inclusione
(
allora la relazione d'ordine è l'inclusione
(![]() ) ed evidentemente
) ed evidentemente ![]() e
e ![]() sono rispettivamente il minimo ed
il massimo di
sono rispettivamente il minimo ed
il massimo di ![]() (se
(se ![]() allora
allora
![]() ossia
ossia
![]() ). Quindi il reticolo è limitato. Che sia
distributivo segue dal fatto che le operazioni
). Quindi il reticolo è limitato. Che sia
distributivo segue dal fatto che le operazioni ![]() e
e ![]() sono
distributive. Proviamo che ogni elemento ha un complemento. Se
sono
distributive. Proviamo che ogni elemento ha un complemento. Se ![]() consideriamo
consideriamo
![]() . Allora chiaramente
. Allora chiaramente ![]() ed
inoltre:
ed
inoltre:
Soluzione dell'esercizio 4 Proviamo che ![]() è un sottoanello dell'anello delle matrici. Evidentemente
è un sottoanello dell'anello delle matrici. Evidentemente
![]() (si ottiene ponendo
(si ottiene ponendo ![]() ) resta da provare che se
che se
) resta da provare che se
che se ![]() allora
allora ![]() ,
, ![]() ,
, ![]() .
Cominciamo dall'ultima sia
.
Cominciamo dall'ultima sia
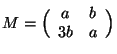 allora
allora
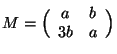 ,
,
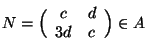 allora
allora
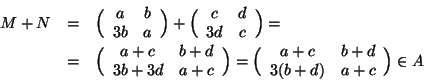
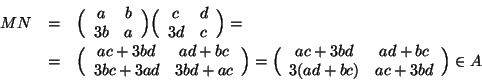
![]() è commutativo. Si osservi infatti che l'espressione per
è commutativo. Si osservi infatti che l'espressione per ![]() che abbiamo
trovato sopra, resta invariata se si scambiano
che abbiamo
trovato sopra, resta invariata se si scambiano ![]() con
con ![]() e
e ![]() con
con ![]() ossia
ossia
![]() .
.
![]() è un campo. Osserviamo innanzitutto che la matrice
è un campo. Osserviamo innanzitutto che la matrice
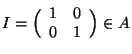 (si ottiene ponendo
(si ottiene ponendo
![]() e
e ![]() ), quindi
), quindi ![]() è un anello unitario.
è un anello unitario.
Una matrice è invertibile se e solo se il suo determinante è diverso da
![]() , ma se
, ma se
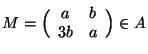 allora
allora
![]() e quindi
e quindi ![]() se e solo se
se e solo se ![]() e
quindi o
e
quindi o ![]() e
e ![]() (ossia
(ossia ![]() ) oppure
) oppure
![]() . Dato che
. Dato che
![]() allora
allora
![]() mentree
mentree
![]() e quindi
l'ultima eventualità non si può verificare. In altre parole se
e quindi
l'ultima eventualità non si può verificare. In altre parole se ![]() e
e
![]() allora
allora ![]() è invertibile. Un semplice calcolo mostra che in questo
caso
è invertibile. Un semplice calcolo mostra che in questo
caso
Consideriam o l'applicazione
![]() definita da
definita da
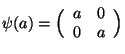 . È immediato
verificare che
. È immediato
verificare che ![]() è un morfismo di anelli con identità, quindi per la
proprietà universale dell'anello dei polinomi, esiste un unico morfismo
è un morfismo di anelli con identità, quindi per la
proprietà universale dell'anello dei polinomi, esiste un unico morfismo
![]() tale che
tale che
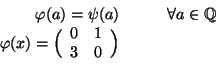
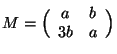 con
con
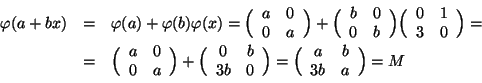
Proviamo che
![]() . Osserviamo innanzitutto che
. Osserviamo innanzitutto che
![]() , infatti
, infatti
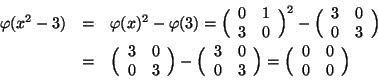
Viceversa, sia
![]() , effettuando la divisione
euclidea di
, effettuando la divisione
euclidea di ![]() per
per ![]() si determinano
si determinano
![]() tali che
tali che
![]() con
con ![]() , ossia
, ossia ![]() . Ma allora
. Ma allora
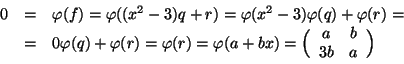
Ma allora per il primo teorema di omomorfismo
Soluzione dell'esercizio 5 Indichiamo con ![]() l'insieme in questione.
Osserviamo che, per il ``lemma dei cassetti'', se un numero
l'insieme in questione.
Osserviamo che, per il ``lemma dei cassetti'', se un numero ![]() ha un
espansione decimale con più di
ha un
espansione decimale con più di ![]() cifre allora almeno due cifre sono
uguali, quindi l'insieme
cifre allora almeno due cifre sono
uguali, quindi l'insieme ![]() è contenuto nell'insieme
è contenuto nell'insieme ![]() dei numeri con
espansione di al più
dei numeri con
espansione di al più ![]() cifre, e quest'ultimo è finito in quanto
cifre, e quest'ultimo è finito in quanto
![]() ha
ha ![]() elementi.
elementi.
Per ogni
![]() indichiamo con
indichiamo con ![]() l'insieme dei numeri diversi da
l'insieme dei numeri diversi da
![]() costituiti
da
costituiti
da ![]() cifre distinte. Chiaramente
cifre distinte. Chiaramente
![]() e
e
![]() se
se ![]() ,
,
![]() per ogni
per ogni ![]() e quindi
e quindi
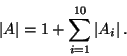
Calcoliamo
![]() per ogni
per ogni ![]() . Se
. Se ![]() è diverso da
è diverso da ![]() , allora
la sua prima cifra può essere un arbitrario numero
, allora
la sua prima cifra può essere un arbitrario numero ![]() (lo
(lo ![]() non
può essere la cifra iniziale) e quindi per la sua scelta si hanno
non
può essere la cifra iniziale) e quindi per la sua scelta si hanno ![]() possibilità. Fissata la prima cifra, le restanti
possibilità. Fissata la prima cifra, le restanti ![]() possono essere scelte
tra le rimanenti
possono essere scelte
tra le rimanenti ![]() cifre in modo che siano a due a due diverse, ossia in
modo che l'applicazione che ad ognuno degli
cifre in modo che siano a due a due diverse, ossia in
modo che l'applicazione che ad ognuno degli ![]() ``posti vuoti'' associa una
di queste
``posti vuoti'' associa una
di queste ![]() cifre sia iniettiva. Quindi fatta la prima scelta si hanno
cifre sia iniettiva. Quindi fatta la prima scelta si hanno
![]() scelte possibili: tante quante le applicazioni iniettive da un
insieme di
scelte possibili: tante quante le applicazioni iniettive da un
insieme di ![]() elementi in uno di
elementi in uno di ![]() elementi. In definitiva
elementi. In definitiva