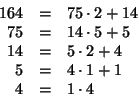
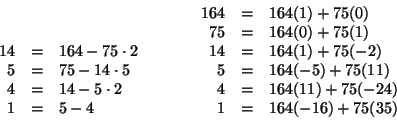
Soluzione dell'esercizio 2 Il polinomio caratteristico è dato da ![]() le cui radici sono
le cui radici sono ![]() e
e
![]() , quindi una base dello spazio delle soluzioni è data dalle due
successioni
, quindi una base dello spazio delle soluzioni è data dalle due
successioni ![]() e
e ![]() , quindi la soluzione generale
dell'equazione è data da:
, quindi la soluzione generale
dell'equazione è data da:
Soluzione dell'esercizio 3 Siano
![]() quindi esistono
quindi esistono
![]() tali che
tali che
![]() . Ma allora
. Ma allora
Evidentemente ![]() , dato che
, dato che ![]() .
.
Se ![]() allora
allora
![]() . Infatti esiste
. Infatti esiste
![]() tale
che
tale
che ![]() , ma allora
, ma allora
![]() .
.
Coò basta per concludere, dato che il prodotto di numeri complessi è associativo.
![]()
Soluzione dell'esercizio 4 (1)![]() (2). Supponiamo che
(2). Supponiamo che ![]() ,
ossia, per definizione di ordinamento indotto,
,
ossia, per definizione di ordinamento indotto,
![]() . Dato che
. Dato che ![]() si ha:
si ha:
(2)![]() (1). Supponiamo che
(1). Supponiamo che ![]() ,
allora
,
allora ![]() e quindi, per (2), si ha che o
e quindi, per (2), si ha che o ![]() oppure
oppure
![]() e quindi
e quindi
![]() .
.
Proviamo olra il secondo punto. Se ![]() è un'algebra di Boole finita, allora,
per il teorema di rappresentazione, è isomorfa all'algebra di Boole
è un'algebra di Boole finita, allora,
per il teorema di rappresentazione, è isomorfa all'algebra di Boole ![]() delle
parti di un insieme finito
delle
parti di un insieme finito ![]() . Per il punto precedente, gli atomi sono allora i
sottoinsiemi
. Per il punto precedente, gli atomi sono allora i
sottoinsiemi ![]() di
di ![]() che non contengono alcun sottoinsieme diverso da
che non contengono alcun sottoinsieme diverso da
![]() ossia sono i sottoinsiemi costituiti da un solo elemento, e quindi sono
tanti quanti gli elementi di
ossia sono i sottoinsiemi costituiti da un solo elemento, e quindi sono
tanti quanti gli elementi di ![]() . In definitiva se
. In definitiva se
![]() ha
ha ![]() elementi,
elementi,
![]() e quindi gli atomi di
e quindi gli atomi di ![]() sono
sono
![]() .
.
![]()
Soluzione dell'esercizio 5 Proviamo che ![]() è un sottoanello dell'anello delle matrici. Evidentemente
è un sottoanello dell'anello delle matrici. Evidentemente
![]() (si ottiene ponendo
(si ottiene ponendo ![]() ) resta da provare che se
che se
) resta da provare che se
che se ![]() allora
allora ![]() ,
, ![]() ,
, ![]() .
Cominciamo dall'ultima sia
.
Cominciamo dall'ultima sia
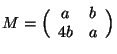 allora
allora
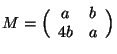 ,
,
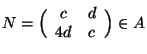 allora
allora
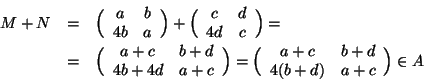
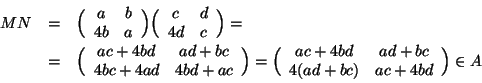
![]() è commutativo. Si osservi infatti che l'espressione per
è commutativo. Si osservi infatti che l'espressione per ![]() che abbiamo
trovato sopra, resta invariata se si scambiano
che abbiamo
trovato sopra, resta invariata se si scambiano ![]() con
con ![]() e
e ![]() con
con ![]() ossia
ossia
![]() .
.
![]() non è un dominio. Osserviamo infatti che
non è un dominio. Osserviamo infatti che