Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 1999/2000
Matematica Discreta (II modulo)
quinto appello, a.a. 1999/2000
22 gennaio 2001
Esercizio 1
Si consideri la funzione
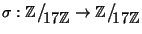
definita da
![$\sigma(\left[x\right])=\left[13\right]\left[x\right]$](img3.gif)
. Dopo aver dimostrato che
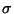
è una
permutazione, se ne trovi la decomposizione in cicli disgiunti. Si dica infine
qual'è il minimo
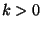
tale che
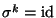
.
Soluzione
Esercizio 2
Sia
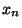
la successione definita per ricorrenza da:
- Provare che
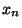 è dispari per ogni
è dispari per ogni 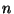
- Determinare il massimo comun divisore
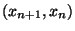 per ogni
per ogni 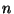 .
.
Soluzione
Esercizio 3
Siano
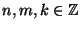
. Si provi che se
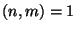
allora
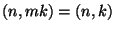
. Dire,
motivando la risposta se è vero il viceversa.
Soluzione
Esercizio 4
Si provi che se un albero ha un vertice di grado
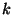
, allora ha almeno
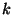
foglie.
Dire, motivando la risposta con una dimostrazione o un contresempio, se è
vero il viceversa.
Soluzione
Esercizio 5
Siano
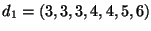
e
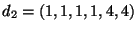
. Dire in quale dei due casi
esiste un grafo
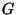
tale che
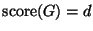
. In caso di risposta affermativa,
dire se un tale grafo
- può essere sconnesso
- può essere senza cicli
Soluzione
Esercizio 6
Dire quali tra i grafi rappresentati in figura sono tra loro isomorfi e quali
no:
Soluzione



Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 1999/2000
Luminati Domenico
2002-05-16