Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 2000/2001
Matematica Discreta (II modulo)
Primo appello, a.a. 2000/2001
13 giugno 2001
Da svolgersi in tre ore. Al candidato si richiede di svolgere cinque (e non
più di cinque) dei sei esercizi. A chi deve recuperare una delle
prove in itinere, si richiede di svolgere tutti gli esercizi della
corrispondente parte e di rispondere alla domanda di teoria.
Esercizio 1
Dire se il sistema di congruenze
ammette soluzioni ed in tal caso determinarle.
Soluzione
Esercizio 2
Si determinino le soluzioni della congruenza
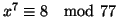
.
Soluzione
Esercizio 3
Sia
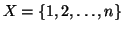
con
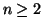
.
- Si determini la cardinalità dell'insieme
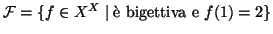 .
.
Sia
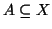
e sia
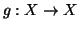
una funzione bigettiva.
- Si determini la cardinalità dell'insieme
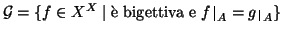 .
.
Soluzione
Domanda di teoria.
Si dia la definizione di elemento invertibile in
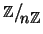 , quindi si enunci e
si provi il piccolo teorema di Fermat.
, quindi si enunci e
si provi il piccolo teorema di Fermat.
Esercizio 4
Sia
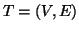
un albero e per ogni
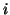
si denoti con
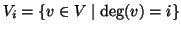
.
Si provi che se 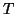 ha solo verici di grado
ha solo verici di grado 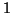 e
e 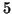 allora
allora
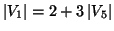 .
.
Dire motivando la risposta se è vero il viceversa.
Soluzione
Esercizio 5
Dire, motivando la risposta, quale dei vettori
è lo score di un grafo e quando ciò è possibile costruire un tale
grafo. Si dica inoltre se
- è possibile trovare un tale grafo che sia anche un albero
- è possibile trovare un tale grafo che sia anche 2-connesso
Soluzione
Esercizio 6
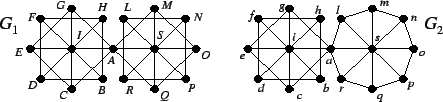
Dire, motivando la risposta, se i due grafi rappresentati in figura sono
tra loro isomorfi oppure no.
Soluzione
Domanda di teoria.
Si dia la definizione di grafo 2-connesso, quindi si provi che in un grafo
2-connesso ogni coppia di vertici è contenuta in un ciclo..



Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 2000/2001
Luminati Domenico
2002-05-16
![]() , quindi si enunci e
si provi il piccolo teorema di Fermat.
, quindi si enunci e
si provi il piccolo teorema di Fermat.
![]() ha solo verici di grado
ha solo verici di grado ![]() e
e ![]() allora
allora
![]() .
.