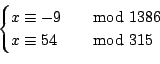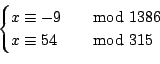Matematica Discreta (II modulo)

Primo appello, a.a. 2004/2005 -- compito 2

Date: 21 giugno 2005

Da svolgersi in tre ore. Al candidato si richiede di svolgere almeno un esercizio di ciascuno dei due gruppi e di rispondere ad almeno una delle domande teoriche. Tutte le risposte devono essere motivate.

Non è ammessa la consultazione di libri e/o appunti.

Esercizio 1   Dire se il seguente sistema di congruenze ammette soluzioni ed in tal caso determinarle tutte:

$$\begin{cases} x\equiv -9 & \quad{\rm mod}\ 1386 \\ x\equiv 54 & \quad{\rm mod}\ 315 \\ \end{cases}$$

    $\square$
Soluzione

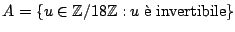
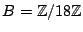
Esercizio 2   Sia $A=\{u \in \mathbb{Z}/ 18\mathbb{Z}:u \;\textrm{\\lq e invertibile} \}$ e $B=\mathbb{Z}/ 18\mathbb{Z}$. Determinare la cardinalità dei seguenti insiemi:

1. $\{f\in B^{A}: \;\textrm{f \\lq e iniettiva}\}$.
2. $\{f\in B^{A}: \;\textrm{f \\lq e iniettiva}, f(\bar 1)=\bar{0}\}$.
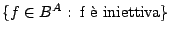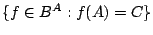3. $\{f\in B^{A}: f(A)=C \}$, essendo $C = \{\bar 2, \bar 3\}$.

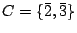Soluzione

Esercizio 3   Dire, motivando la risposta, quale dei vettori

$$d_1 = (1, 1, 1, 1, 2, 2, 2, 2, 7, 9)\qquad d_2 = (2, 2, 3, 3, 4, 4, 7, 7)$$

è lo score di un grafo e quando ciò è possibile costruire un tale grafo. Si dica inoltre se

1. è possibile trovare un tale grafo che sia anche un albero
2. è possibile trovare un tale grafo che sia sconnesso
3. è possibile trovare un tale grafo che sia 2-connesso

Soluzione

Esercizio 4   Dire, motivando la risposta, quali tra i grafi rappresentati in figura sono tra loro isomorfi e quali no.

Soluzione

Domanda di teoria 1.  Si enunci e si provi il teorema di rappresentazione dei numeri naturali in una base fissata. Si descriva un algoritmo ricorsivo per trovare la rappresentazione in una data base di un numero.

Domanda di teoria 2. Si dia la definizione di albero, quindi si enunci e si provi il teorema di caratterizzazione degli alberi finiti (formula di Eulero).