Soluzione dell'esercizio 2 (1).
Soluzione dell'esercizio 2 (1).
![]() se e solo se
se e solo se
![]() . Dato che gli unici tre
numeri consecutivi il cui prodotto fa
. Dato che gli unici tre
numeri consecutivi il cui prodotto fa ![]() sno
sno ![]() ,
, ![]() e
e ![]() , si ha
che
, si ha
che ![]() .
.
Per le altre risposte si veda la soluzione dell'altro compito di
questo appello.
![]()
Soluzione dell'esercizio 3 Se ![]() è un grafo tale che
è un grafo tale che
![]() allora
allora
![]() e ci sono due vertci di grado
e ci sono due vertci di grado ![]() , chiamiamoli
, chiamiamoli ![]() e
e ![]() . Ma allora i
vertci che sono adiacenti sia a
. Ma allora i
vertci che sono adiacenti sia a ![]() che a
che a ![]() devono essere almeno
devono essere almeno ![]() (in un insieme con
(in un insieme con ![]() elementi due sottinsiemi dicardinalità
elementi due sottinsiemi dicardinalità ![]() hanno intersezione di cardinalità almeno
hanno intersezione di cardinalità almeno ![]() ) e quindi ci dovrebbero
essere almeno
) e quindi ci dovrebbero
essere almeno ![]() vertici diversi da
vertici diversi da ![]() e
e ![]() con grado almeno
con grado almeno
![]() . Ciò è in contraddizione con il fatto che di vertici di grado
. Ciò è in contraddizione con il fatto che di vertici di grado
![]() e diversi da
e diversi da ![]() e
e ![]() ce ne dovrebbero essere soltanto
ce ne dovrebbero essere soltanto ![]() .
.
Per ![]() usiamo il teorema dello score:
usiamo il teorema dello score:
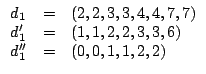
 |
(1).
La risposta è no. Ogni albero finito havertici di grado ![]() , mentre
in un tale grafo ogni vertice ha grado
, mentre
in un tale grafo ogni vertice ha grado ![]() .
.
(2).
La risposta è no. Se ![]() è un grafo tale che
è un grafo tale che
![]() allora
esiste
allora
esiste ![]() tale che
tale che ![]() , ossia ogni altro vertice gli è
adiacente. Quindi
, ossia ogni altro vertice gli è
adiacente. Quindi ![]() è connesso.
è connesso.
(3).
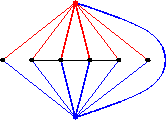
Che il grafo di figura 1 sia ![]() -connesso lo si può
vedere ad esempio mostrando che è ottenuto da un ciclo con
successive aggiunzioni e suddivisioni di lati.
-connesso lo si può
vedere ad esempio mostrando che è ottenuto da un ciclo con
successive aggiunzioni e suddivisioni di lati.
![]()
Soluzione dell'esercizio 4 Il primo ed il terzo grafo sono tra loro isomorfi e contengono
evidentemente dei ![]() -cicli. Il secondo non contiene
-cicli. Il secondo non contiene ![]() -cicli (per
una motivazione si veda la soluzione dell'altro compito di questo
appello) e quindi non è isomorfo agli altri due.
-cicli (per
una motivazione si veda la soluzione dell'altro compito di questo
appello) e quindi non è isomorfo agli altri due.
![]()