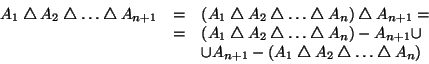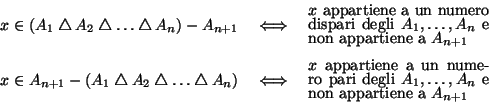Supponiamo la tesi vera per ![]() e proviamola per
e proviamola per ![]() .
.
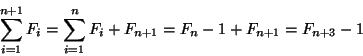
Soluzione dell'esercizio 2 Poiché
![]() , la seconda congruenza è equivalente a
, la seconda congruenza è equivalente a
![]() , e quindi il sistema equivale a:
, e quindi il sistema equivale a:
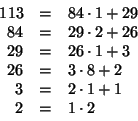
Esprimiamo ![]() come combinazione intera di
come combinazione intera di ![]() e
e ![]() .
.
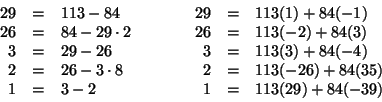
Soluzione dell'esercizio 3 L'operazione è associativa. Infatti:
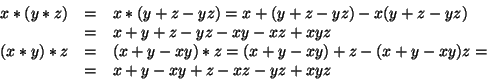
C'è l'elemento neutro. Infatti:
![]() non è un gruppo, dato che
non è un gruppo, dato che ![]() non ha inverso. Infatti per ogni
non ha inverso. Infatti per ogni
![]() si ha:
si ha:
Soluzione dell'esercizio 4 Denotiamo
![]() . Ovviamente la permutazione
identica
. Ovviamente la permutazione
identica ![]() , dato che fissa tutti gli elementi. Siano
, dato che fissa tutti gli elementi. Siano
![]() allora, dato che
allora, dato che ![]() e
e ![]() anche
anche
![]() e quindi:
e quindi:
Soluzione dell'esercizio 5 L'operazione è associativa. Infatti:
![]() è unità sinistra e destra. Infatti
è unità sinistra e destra. Infatti
Ogni elemento è invertibile. Infatti se ![]() allora
allora
![]() e
e
![]() è un sottogruppo. Infatti,
è un sottogruppo. Infatti, ![]() . Inoltre se
. Inoltre se
![]() allora
allora
![]() non è sottogruppo. Infatti non è chiuso per l'operazione. Ad esempio
non è sottogruppo. Infatti non è chiuso per l'operazione. Ad esempio
![]() ma
ma
![]() .
.
![]() non è sottogruppo. Infatti non è detto che ogni elemento di
non è sottogruppo. Infatti non è detto che ogni elemento di ![]() abbia inverso in
abbia inverso in ![]() . Ad esempio
. Ad esempio ![]() mentre
mentre
![]() .
.
![]()
Soluzione dell'esercizio 6 Procediamo per induzione su ![]() . Per
. Per ![]() la tesi segue immediatamente dalla
definizione di differenza simmetrica.
la tesi segue immediatamente dalla
definizione di differenza simmetrica.
Supponiamo la tesi vera per ![]() , allora
, allora