


Next: Soluzioni proposte
Previous: Matematica Discreta 1998/99
Matematica Discreta (I modulo)
Primo appello, a.a. 1998/99
7 giugno 1999
Da svolgersi in tre ore, senza l'ausilio di appunti e/o libri.
Si ricorda che, anche se non esplicitamente richiesto nei testi, tutte le
risposte alle domande devono essere adeguatamente motivate con
dimostrazioni o confutazioni.
Esercizio 1
Si determini la soluzione dell'equazione ricorsiva lineare
con dati iniziali
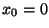
,
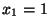
,
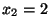
.
Soluzione
Esercizio 2
Sia
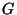
un gruppo si definisca
- Si provi che
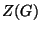 è un sottogruppo di
è un sottogruppo di 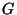 .
.
- Si dica, motivando la risposta, se
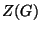 è normale.
è normale.
- Si determini
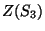 .
.
Soluzione
Esercizio 3
Siano
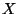
un insieme e
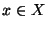
un suo elemento. Si ponga
Si dica, motivando la risposta, se
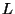 , con le operazioni di
, con le operazioni di 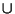 e
e 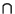 (unione e intersezione) è
un reticolo.
(unione e intersezione) è
un reticolo.
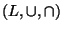 è un sottoreticolo di
è un sottoreticolo di
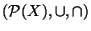 .
.
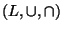 è un'algebra di Boole.
è un'algebra di Boole.
Soluzione
Esercizio 4
Si consideri l'insieme
Si dica, motivando la risposta, se con le operazioni di somma e prodotto di
matrici
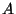 è un anello.
è un anello.
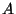 è commutativo.
è commutativo.
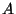 è un campo.
è un campo.
Si provi che esiste un morfismo surgettivo
![$\varphi :\mathbb{Q}[x]\to A$](img20.gif)
tale che
Si usi questo fatto per provare che
![$A\oldcong \mathbb{Q}[x]\big/\mathchoice
{{}_{\!\displaystyle {}(x^2-3)}}
{{}_...
...^2-3)}}
{{}_{\!\scriptstyle {}(x^2-3)}}
{{}_{\!\scriptscriptstyle {}(x^2-3)}}$](img22.gif) Soluzione
Soluzione
Esercizio 5
Si provi che l'insieme dei numeri naturali le cui cifre (nella usuale
scrittura decimale) sono tutte diverse è finito e se ne determini il
numero di elementi.
Soluzione



Next: Soluzioni proposte
Previous: Matematica Discreta 1998/99
Luminati Domenico
2002-05-16