Supponiamo che la formula valga per ![]() , allora
, allora
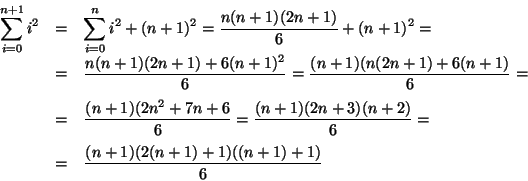
Soluzione dell'esercizio 2 Il polinomio caratteristico è dato da ![]() le cui radici sono
le cui radici sono ![]() e
e
![]() , quindi una base dello spazio delle soluzioni è data dalle due
successioni
, quindi una base dello spazio delle soluzioni è data dalle due
successioni ![]() e
e ![]() , quindi la soluzione generale
dell'equazione è data da:
, quindi la soluzione generale
dell'equazione è data da:
Soluzione dell'esercizio 3 ![]() in quanto
in quanto
![]() per ogni
per ogni
![]() .
.
Siano
![]() , allora
, allora
Sia ![]() allora
allora
Se ![]() proviamo che
proviamo che
![]() . Infatti se
. Infatti se ![]() allora, dato che
allora, dato che
![]() è un sottogruppo,
è un sottogruppo,
![]() e quindi
e quindi
![]() . D'altra parte se
. D'altra parte se ![]() allora
allora
![]() e quindi
e quindi
![]() , ossia
, ossia
![]() e, per tanto
e, per tanto
![]() , ossia
, ossia ![]() .
.
Ricordiamo che uno dei modi equivalenti di dire che ![]() è normale in
è normale in ![]() è
che
è
che ![]() per ogni
per ogni ![]() e quindi se e solo se
e quindi se e solo se ![]() per
ogni
per
ogni ![]() ovvero se e solo se
ovvero se e solo se ![]() .
.
![]()
Soluzione dell'esercizio 4 Osserviamo che se ![]() è una sottoalgebra che contiene sia
è una sottoalgebra che contiene sia ![]() che
che ![]() ,
allora anche
,
allora anche ![]() e quindi per ogni
e quindi per ogni ![]() si ha che
si ha che
![]() ,
,
![]() e quindi anche
e quindi anche
![]() , ossia
, ossia
![]() . Basta allora provare che
. Basta allora provare che ![]() è una sottoalgebra, ossia che
è chiusa rispetto a
è una sottoalgebra, ossia che
è chiusa rispetto a ![]() ,
, ![]() e
e ![]() e che contiene
e che contiene ![]() .
.
Dato che ![]() è una sottoalgebra,
è una sottoalgebra, ![]() e quindi
e quindi
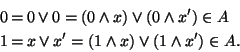
Siano
![]() ,
,
![]() , allora
, allora
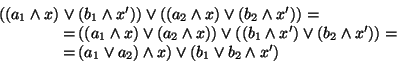
Siano
![]() ,
,
![]() , allora
, allora
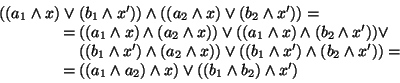
Sia
![]() , allora
, allora
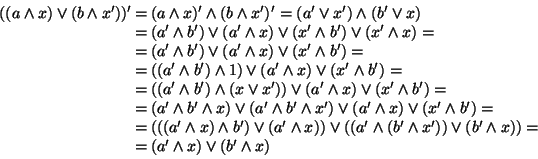
Soluzione dell'esercizio 5 L'unità dell'anello
![]() è
è
![]() . Ma allora, perché
un elemento
. Ma allora, perché
un elemento
![]() sia invertibile, dovranno essere
invertibili entrambe le sue coordinate, e quindi, dato che
sia invertibile, dovranno essere
invertibili entrambe le sue coordinate, e quindi, dato che ![]() e
e ![]() sono
campi, ciò equivale a dire che entrambe le coordinate siano diverse da
sono
campi, ciò equivale a dire che entrambe le coordinate siano diverse da
![]() . Quindi l'insieme degli elementi invertibili è dato da:
. Quindi l'insieme degli elementi invertibili è dato da:
Proviamo che
![]() possiede soltanto i quattro ideali:
possiede soltanto i quattro ideali:
![]() ,
,
![]() ,
,
![]() e
e
![]() . Proviamo innanzitutto che
. Proviamo innanzitutto che
![]() e
e
![]() sono ideali. Sono ovviamente chiusi rispetto
alla somma, inoltre se
sono ideali. Sono ovviamente chiusi rispetto
alla somma, inoltre se
![]() e
e
![]() allora
allora
![]() , e analogamente per l'altro
ideale.
, e analogamente per l'altro
ideale.
Proviamo ora che non ci sono altri ideali. Sia ![]() un ideale non banale di
un ideale non banale di
![]() (ossia
(ossia
![]() e
e
![]() ). Sia
). Sia
![]() . Se
. Se ![]() e
e ![]() sono entrambi non nulli allora
sono entrambi non nulli allora ![]() è
invertibile e quindi
è
invertibile e quindi
![]() , contro l'assunto (ricordiamo che se un
ideale contiene un elemento invertibile, allora coincide con tutto l'anello).
Supponiamo che
, contro l'assunto (ricordiamo che se un
ideale contiene un elemento invertibile, allora coincide con tutto l'anello).
Supponiamo che ![]() , allora
, allora
![]() e quindi per ogni
e quindi per ogni
![]() si ha che
si ha che
![]() e quindi
e quindi
![]() . D'altra parte se esistesse un elemento
. D'altra parte se esistesse un elemento ![]() con
con ![]() allora
allora
![]() sarebbe un elemento invertibile e quindi
sarebbe un elemento invertibile e quindi
![]() , contro quanto supposto, per tanto
, contro quanto supposto, per tanto
![]() .
.
In modo analogo si prova che se ![]() allora
allora
![]() .
.
![]()