


Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 2000/2001
Matematica Discreta, II modulo
Prima prova in itinere, a.a. 2000/2001
27 aprile 2001
Da svolgersi in tre ore. Si richiede che vengano svolti a scelta quattro (e non
più di qyuattro) dei cinque esercizi e che si risponda alla domanda di teoria.
Esercizio 1
Siano
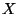
,
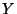
,
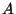
insiemi. Si provi che
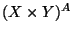
è in corrispondenza
biunivoca con
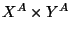
.
Soluzione
Esercizio 2
Siano
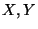
insiemi finiti, e
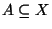
,
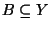
. Posto
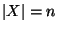
,
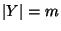
,
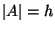
e
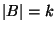
si determini, in funzione di
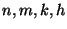
la cardinalità degli insiemi
[Suggerimento per il primo punto: si osservi che
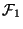
è il
complementare di
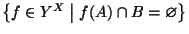
.]
Soluzione
Esercizio 3
Dire se il sistema di congruenze
Soluzione
Esercizio 4
Si determinino le soluzioni della congruenza
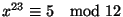
.
Soluzione
Esercizio 5
Sia
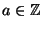
e
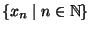
una successione di interi tali che
Si provi che allora
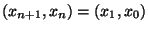
per ogni
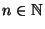
.
Supponendo che 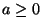 e che
e che 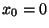 e
e 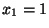 si provi che
si provi che
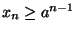 per ogni
per ogni 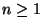 .
.
Soluzione
Domanda di teoria.
Si dia la definizione di massimo comun divisore tra numeri interi e si enunci
e si dimostri il teorema di esistenza e unicità del massimo comun divisore.



Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 2000/2001
Luminati Domenico
2002-05-16

![]() e che
e che ![]() e
e ![]() si provi che
si provi che
![]() per ogni
per ogni ![]() .
.