Dim.
Dimostriamo l'esistenza. Se ![]() e m>0 la tesi segue dalla proposizione
1.4 e dall'osservazione che
e m>0 la tesi segue dalla proposizione
1.4 e dall'osservazione che
![]() .
.
Supponiamo ora n<0 e m>0. Allora -n>0 e quindi per il caso
precedente si ha che esistono
![]() tali che -n=mq+r e
tali che -n=mq+r e
![]() .
E quindi n=m(-q)-r. Se r=0 abbiamo finito, se invece
0<r<m allora
.
E quindi n=m(-q)-r. Se r=0 abbiamo finito, se invece
0<r<m allora
![]() e
n=m(-q)-r=m(-q)-m+m-r=m(-1-q)+(m-r).
e
n=m(-q)-r=m(-q)-m+m-r=m(-1-q)+(m-r).
Sia infine m<0 allora -m>0, quindi per i due casi precedenti
esistono
![]() tali che
n=(-m)q+=m(-q)+r con
tali che
n=(-m)q+=m(-q)+r con
![]() .
.
Dimostriamo ora l'unicità. Supponiamo che
n=mq+r=mq'+r' con
![]() .
Supponiamo che
.
Supponiamo che ![]() ,
allora
m(q-q')=r'-r e
quindi passando ai moduli si ha
,
allora
m(q-q')=r'-r e
quindi passando ai moduli si ha
![]() ,da cui
,da cui
![]() e quindi
e quindi
![]() ovvero q=q'. Ma
allora da
mq+r=mq'+r' segue che anche r=r'.
ovvero q=q'. Ma
allora da
mq+r=mq'+r' segue che anche r=r'.
![]()
Dim.
Dimostriamo l'esistenza per induzione su n. Se n=0 basta prendere
![]() per ogni
per ogni
![]() .
Supponiamo ora n>0 e che la tesi sia
vera per ogni k<n. Siano q,r tali che n=bq+r con
.
Supponiamo ora n>0 e che la tesi sia
vera per ogni k<n. Siano q,r tali che n=bq+r con ![]() .
Dato che
.
Dato che ![]() si ha che
si ha che
![]() e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
![]() ,
costituita di interi tali che
,
costituita di interi tali che
![]() per
ogni i e tale che
per
ogni i e tale che
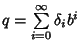 .
Ma
allora
.
Ma
allora
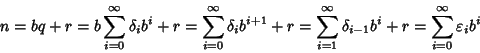
Dimostriamo ora l'unicità. Procediamo per induzione su n. Se
![]() allora ogni addendo della somma essendo
nonnegativo, deve essere nullo e quindi
allora ogni addendo della somma essendo
nonnegativo, deve essere nullo e quindi
![]() per ogni i.
per ogni i.
Supponiamo ora n>0 e che l'espressione in base b sia unica per
tutti i numeri k<n. Sia n tale che
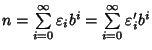 .
Allora possiamo scrivere
.
Allora possiamo scrivere
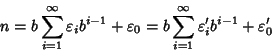
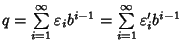 .
Come prima q<n e quindi per ipotesi di induzione si ha anche che
.
Come prima q<n e quindi per ipotesi di induzione si ha anche che