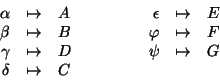Determiniamo ![]() .
.
![]() , quindi
, quindi ![]() . Ma allora la
soluzione è data da
. Ma allora la
soluzione è data da
![]() .
.
![]()
Soluzione dell'esercizio 2 (1). Per induzione. Per ![]() è ovvio dalla definizione. Sia
è ovvio dalla definizione. Sia ![]() e
supponiamo che la tesi sia vera per ogni
e
supponiamo che la tesi sia vera per ogni ![]() , allora
, allora
![]() è somma di un numero pari (
è somma di un numero pari (![]() ) e di un numero,
) e di un numero, ![]() , che, per
ipotesi di induzione, è dispari. Quindi
, che, per
ipotesi di induzione, è dispari. Quindi ![]() è dispari.
è dispari.
(2). Per induzione. Se ![]() ,
,
![]() . Supponiamo la
tesi vera per
. Supponiamo la
tesi vera per ![]() e proviamola per
e proviamola per ![]() . Dalla relazione di ricorrenza si ha
che
. Dalla relazione di ricorrenza si ha
che
![]() e per ipotesi di
induzione, quest'ultimo è
e per ipotesi di
induzione, quest'ultimo è ![]() .
.
(3). Il polinomio caratteristico di tale equazione ricorsiva è
dato da ![]() le cui radici sono:
le cui radici sono: ![]() e
e ![]() . Quindi una
generica soluzione della relazione ricorsiva è data da:
. Quindi una
generica soluzione della relazione ricorsiva è data da:
![]() . Determiniamo
. Determiniamo ![]() e
e ![]() in modo che siano verificate le condizioni iniziali.
in modo che siano verificate le condizioni iniziali.
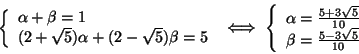
Soluzione dell'esercizio 3 Indichiamo con
![]() . Per ogni
. Per ogni
![]() consideriamo l'applicazione
consideriamo l'applicazione
![]() definita da
definita da
![]() è una permutazione. Basta provare che è iniettiva
(dato che l'insieme di definizione è finito e coincide con il
codominio). Siano
è una permutazione. Basta provare che è iniettiva
(dato che l'insieme di definizione è finito e coincide con il
codominio). Siano ![]() : se
: se ![]() allora
allora
![]() , dato
che
, dato
che ![]() è una permutazione; se
è una permutazione; se ![]() allora
allora
![]() , dato
che
, dato
che ![]() è una permutazione; infine se
è una permutazione; infine se ![]() e
e ![]() allora
allora
![]() e
e
![]() e
e
![]() poiché
poiché
![]() .
.
Osserviamo ora che, per definizione,
![]() , ossia abbiamo
definito una applicazione
, ossia abbiamo
definito una applicazione
![]() . Proviamo che tale
applicazione è bigettiva.
. Proviamo che tale
applicazione è bigettiva.
![]() è iniettiva. Se
è iniettiva. Se
![]() esiste
esiste ![]() tale che
tale che
![]() e quindi
e quindi
![]() e
quindi
e
quindi
![]() .
Analogamente se
.
Analogamente se ![]() allora
allora
![]() .
.
![]() è surgettiva. Sia
è surgettiva. Sia
![]() , allora
, allora
![]() , e dato che
, e dato che ![]() è bigettiva, anche
è bigettiva, anche ![]() e quindi
e quindi
![]() . È immediato allora vedere che
. È immediato allora vedere che
![]() .
.
Ma allora
Soluzione dell'esercizio 4 Sia ![]() un vertice di grado
un vertice di grado ![]() (massimo possibile), allora
(massimo possibile), allora ![]() è un grafo
connesso, quindi contiene un albero generatore
è un grafo
connesso, quindi contiene un albero generatore ![]() (ossia tale che
(ossia tale che
![]() . Ma allora, per la relazione che lega il numero di vertici e il
numero di lati di un albero,
. Ma allora, per la relazione che lega il numero di vertici e il
numero di lati di un albero,
![[*]](crossref.png) si ottiene
si ottiene
Il viceversa non è vero. Si consideri ad esempio il grafo rappresentato in
figura ![[*]](crossref.png) :
:
Soluzione dell'esercizio 5 Usiamo il teorema dello score:
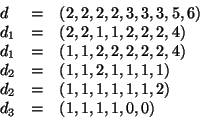
Soluzione dell'esercizio 6 Il primo grafo è hamiltoniano (in particolare quindi è ![]() -connesso) in
quanto c'è il ciclo
-connesso) in
quanto c'è il ciclo
![]() .
.
Il terzo grafo non è ![]() -connesso, infatti se a questo grafo si toglie il
vertice
-connesso, infatti se a questo grafo si toglie il
vertice ![]() si ottengono i due cicli
si ottengono i due cicli ![]() e
e ![]() .
.
Il secondo e il terzo grafo sono isomorfi(quindi il primo e il secondo non lo
sono). Un isomorfismo è dato ad esempio dalla funzione definita da: