


Next: Lezione 16 (9 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 14 (2 maggio
Subsections
Sia
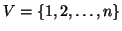 e indichiamo con
e indichiamo con
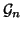 l'insieme dei grafi che
hanno V come insieme dei vertici. Dall'esercizio 14.8 segue che
l'insieme dei grafi che
hanno V come insieme dei vertici. Dall'esercizio 14.8 segue che
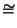 è una relazione d'equivalenza su
è una relazione d'equivalenza su
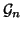 .
Indichiamo con
.
Indichiamo con
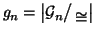 .
.
In parolo povere gn è il massimo numero di grafi di
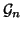 tra loro
non isomorfi. ovvero se si è interessati a sapere quanti sono i grafi
essenzialmente diversi con vertici V il numero interessante è gn.
tra loro
non isomorfi. ovvero se si è interessati a sapere quanti sono i grafi
essenzialmente diversi con vertici V il numero interessante è gn.
Proposizione 15.1
Con le notazioni appena introdotte si ha che
Dimostrazione.

Definizione 15.2
Sia
G=(
V,
E) un grafo una successione finita di vertici
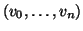
sarà detta
- passeggiata se
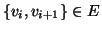 per ogni
per ogni
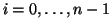
- cammino se è una passeggiata e
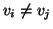 per ogni
per ogni 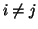 .
.
- ciclo se è una passeggiata e
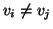 per ogni
per ogni 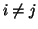 a
parte v0=vn.
a
parte v0=vn.
Proposizione 15.3
Sia
G un grafo e sia
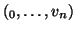
un cammino in
G allora il grafo
G' definito da:
è un sottografo di
G isomorfo a
Pn.
Dimostrazione.
Esercizio.

Proposizione 15.4
Sia
G un grafo e sia
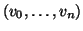
un ciclo in
G allora il grafo
G' definito da:
è un sottografo di
G isomorfo a
Cn.
Dimostrazione.
Esercizio.

Osservazione 15.5
In effetti è facile vedere che dare un cammino o un ciclo in un grafo è
equivalente a dare un sottografo isomorfo a Pn o Cn per qualche n.
Definizione 15.6
Sia
G=(
V,
E) e siano
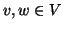
.
Diremo che
v e
w sono
congiungibili con un cammino [risp. una passeggiata] se e siste un
cammino [risp. una passeggiata]
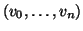
tale che
v0=
v e
vn=
w.
Proposizione 15.7
Le relazione di essere congiungibli da un cammino è una passeggiata
d'equivalenza.
Proposizione 15.8
Due punti sono congiungibili mediante un cammino se e solo se lo sono mediante
una passeggiata.
Dimostrazione.
Dato che un cammino è una passeggiata, se due vertici sono congiungibili
mediante un cammino lo sono anche mediante una passeggiata.
Viceversa. Sia 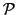




Next: Lezione 16 (9 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 14 (2 maggio
Domenico Luminati
2001-06-18
![]() e indichiamo con
e indichiamo con
![]() l'insieme dei grafi che
hanno V come insieme dei vertici. Dall'esercizio 14.8 segue che
l'insieme dei grafi che
hanno V come insieme dei vertici. Dall'esercizio 14.8 segue che
![]() è una relazione d'equivalenza su
è una relazione d'equivalenza su
![]() .
Indichiamo con
.
Indichiamo con
![]() .
.
![]() tra loro
non isomorfi. ovvero se si è interessati a sapere quanti sono i grafi
essenzialmente diversi con vertici V il numero interessante è gn.
tra loro
non isomorfi. ovvero se si è interessati a sapere quanti sono i grafi
essenzialmente diversi con vertici V il numero interessante è gn.
![]()
![]()
![]()
![]()
![]()