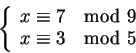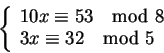Next: Grafi
Up: Esercizi
Previous: Calcolo combinatorio
Esercizio 3.1
Trovare
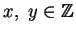
tali che
1= 15
x + 26
y.
Esercizio 3.2
Trovare
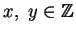
tali che
33
x+ 50
y = 24
Esercizio 3.4
Calcolare il resto della divisione di 10! per 11.
Esercizio 3.5
Dire se il seguente sistema di congruenze:
ammette soluzioni, e in caso positivo determinarle.
Esercizio 3.6
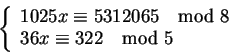
Si risolva il seguente sistema di congruenze:
Esercizio 3.7
Si risolva il seguente sistema di congruenze:
Esercizio 3.8
Si determinino gli invertibili di
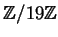
e si trovi l'inverso di ogni
invertibile.
Esercizio 3.9
Si trovino gli inversi degli elementi invertibili di
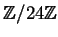
.
Domenico Luminati
2001-05-21