


Next: About this document ...
Up: Esercizi
Previous: Congruenze
Esercizio 4.1
Sia G un grafo regolare con 8 vertici e 16 lati. Dire qual è il grado comune di tutti i vertici. Sapendo inoltre che G è un grafo bipartito completo, dire il numero dei vertici dei due sottinsiemi in cui è suddiviso l'insieme V(G).
È vero che G è connesso?
Esercizio 4.2
Sia G un grafo con 8 vertici e 2 componenti connesse. Qual è il massimo numero di lati che può avere G?
Disegnare il grafo con il massimo numero di lati.
Se G ha 10 lati, quanti lati ha il complementare di G?
Esercizio 4.3
Sia G un grafo con 7 vertici e 11 lati. Supponiamo inoltre che G abbia due componenti connesse, e che ciascuna componente connessa sia un grafo completo. Trovare il numero di vertici di ogni componente.
È vero che G è bibartito?
Esercizio 4.4
Se un grafo G ha 7 lati e il suo complementare ne ha 8, quanti vertici ha G?
Se un grafo regolare ha 7 lati, quanti vertici ha?
Se G è un grafo con 6 vertici e il suo complementare ha il doppio dei lati di G, quanti lati ha G?
Esercizio 4.5
Mostrare che un grafo
G contiene un triangolo se e solo se esistono
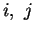
tale che
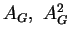
hanno l'entrata (
i,
j) non nulla.
(Con
AG intendo la matrice di adiacenza di
G.)
Esercizio 4.6
Sia G un grafo con almeno due vertici; dimostrare che G contiene due vertici con lo stesso grado.
Esercizio 4.7
Sia G un grafo con 8 vertici e 7 lati. Supponiamo che G abbia un ciclo C di lunghezza 6. È vero che G è sconnesso?
Supponiamo che uno e uno solo dei vertici del ciclo C abbia grado 3.
È vero che G è bipartito?
Esercizio 4.8
Sia
G un grafo con 6 vertici privo di punti isolati. Supponiamo inoltre che
G abbia un lato in più del suo complementare
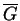
.
Quanti lati ha
G?
È vero che
G è connesso?
Con i dati che abbiamo, è possibile stabilire se
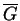
connesso?
Esercizio 4.9
Costruire, se possibile, un grafo bipartito che contenga un sottografo isomorfo
a C7.
Costruire, se possibile un grafo bipartito che contenga un sottografo isomorfo a C6.
Esercizio 4.10
Sia G un grafo con due componenti connesse, sapendo che entrambe le componenti connesse sono complete, cosa si può dire del complementare di G?
Esercizio 4.11
Mostrare che se G è un grafo, c il numero di cicli di lunghezza 3 di G
allora
6c= tr(AG3).
(Con tr(AG3) indico la traccia (somma degli elementi sulla diagonale)
del cubo della matrice di adiacenza di G).
Esercizio 4.12
Mostrare che se due cicli distinti di un grafo G contengono un
lato in comune e, allora esiste un ciclo di G che non contiene e.
Esercizio 4.13
Dire se le stringhe seguenti sono lo score di un grafo e in caso affermativo disegnare un grafo con tale score:
- 1.
-
(2, 3, 3, 3, 1)
- 2.
-
(3,4,4, 3, 1, 4, 1)
- 3.
-
(5, 6, 4, 4, 1, 2, 1)
Nei casi in cui la stringa rappresenta lo score di un grafo dire se esiste
un grafo connesso con tale score.



Next: About this document ...
Up: Esercizi
Previous: Congruenze
Domenico Luminati
2001-05-21