


Next: Soluzioni proposte
Matematica Discreta (II modulo)
Terzo appello, a.a. 2001/2002
Date: 19 settembre 2002
Da svolgersi in tre ore. Al candidato si richiede di svolgere almeno un
esercizio di ciascuno dei due gruppi e di rispondere ad almeno una delle domande
teoriche.
Non è ammessa la consultazione di libri e/o appunti.
Esercizio 1
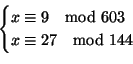
Dire, motivando la risposta, se il sistema di congruenze
ammette soluzioni ed in tal caso determinarle tutte.
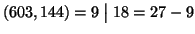
quindi il sistema e` risolubile.
Inoltre
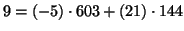
quindi
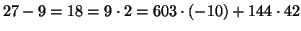
quindi
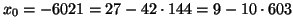
è una soluzione del
sistema. Tutte le soluzioni sono allora date da
![$ \{ -6021 + k [144,603] \mid
k\in\mathbb{Z}\}=\{ -6021 + k 9648 \mid k\in\mathbb{Z}\}=\{ 3627 + k 9648 \mid k\in\mathbb{Z}\} =
\left[3627\right]_{9648}$](img18.gif)

Soluzione
Esercizio 2
Su uno scaffale ci sono
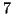
libri,
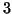
sono libri di matematica e
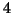
sono libri
di scienze. In quanti modi si possono disporre i libri sullo scaffale perché
tutti i libri di matematica stiano assieme? [Charles M. Schulz]
Sapresti fornire, motivandola, una formula per lo soluzione dello stesso
problema nel caso generale di 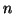 libri di matematica e
libri di matematica e 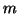 libri di scienze?
libri di scienze?
Soluzione
Esercizio 3
Dire, motivando la risposta, quale dei vettori
è lo score di un grafo e quando ciò è possibile costruire un tale
grafo. Si dica inoltre se
- è possibile trovare un tale grafo che sia anche un albero
- è possibile trovare un tale grafo che sia 2-connesso
- è possibile trovare un tale grafo che sia sconnesso
Soluzione
Esercizio 4
Sia
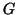
un grafo aciclico con 10 vertici e
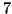
lati. Provare che è possibile
aggiungere a
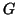
un lato in modo che il grafo rimanga aciclico.
Qual è il massimo numero di lati che si possono aggiungere a 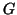 in modo che
rimanga aciclico?
in modo che
rimanga aciclico?
Soluzione
Domanda di teoria 1.
Si dia la definizione di rappresentabilità di un numero naturale rispetto ad
una base fissata. Quindi si enunci e si provi il teorema di
rappresentabilità dei numeri naturali rispetto ad una base fissata.
Domanda di teoria 2.
Scrivere e provare la formula che in un grafo finito lega i gradi dei vertici al
numero dei lati. Se ne enunci quindi qualche conseguenza



Next: Soluzioni proposte
Luminati Domenico
2002-09-19

![]() libri di matematica e
libri di matematica e ![]() libri di scienze?
libri di scienze?
![]() in modo che
rimanga aciclico?
in modo che
rimanga aciclico?