 |
Soluzione dell'esercizio 2 Nella figura 1 c'è la soluzione proposta da Charles M. Schulz.
Il problema può essere affrontato nel modo seguente. Prima si dispongono i
libri di matematica, quindi per ogni
![]() si scelgono
si scelgono ![]() libri di
scienze che si dispongono alla loro sinistra mentre i rimanenti si dispongono
alla loro destra. Contiamo in quanti modi si possono fare queste operazioni.
libri di
scienze che si dispongono alla loro sinistra mentre i rimanenti si dispongono
alla loro destra. Contiamo in quanti modi si possono fare queste operazioni.
Gli ![]() libri di matematica possono essere disposti in
libri di matematica possono essere disposti in ![]() modi. Fissato
modi. Fissato
![]() i
i ![]() libri di scienze da porre alla
sinistra possono essere scelti in
libri di scienze da porre alla
sinistra possono essere scelti in
![]() modi diversi, e questi libri
possono essere permutati n
modi diversi, e questi libri
possono essere permutati n ![]() modi diversi mentre i rimanenti (quelli da
mettere alla destra) possono essere disposti in
modi diversi mentre i rimanenti (quelli da
mettere alla destra) possono essere disposti in ![]() modi diversi. Quindi,
fissata una disposizione di libri di matematica, i libri di scienze possono
essere disposti in
modi diversi. Quindi,
fissata una disposizione di libri di matematica, i libri di scienze possono
essere disposti in
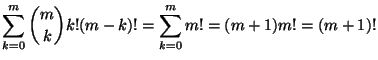
Nel caso del problema di Piperita Patty il risultato è quindi
![]() .
.
![]()
Soluzione dell'esercizio 3 Un grafo ![]() tale che
tale che
![]() dovrebbe avere
dovrebbe avere ![]() vertici, un vertice
vertici, un vertice
![]() di grado
di grado ![]() (ovvero collegato a tutti gli altri) ed un vertice
(ovvero collegato a tutti gli altri) ed un vertice ![]() di
grado
di
grado ![]() . Ne consegue che l'insieme dei vertici collegati ad entrambi questi
due vertici ha almeno
. Ne consegue che l'insieme dei vertici collegati ad entrambi questi
due vertici ha almeno ![]() elementi. D'altra parte
elementi. D'altra parte
![]() e
e
![]() e quindi l'insieme dei vertici che ha cardinalità almeno
e quindi l'insieme dei vertici che ha cardinalità almeno ![]() deve avere almeno
deve avere almeno ![]() elementi e pertanto al massimo un vertice può avere
grado
elementi e pertanto al massimo un vertice può avere
grado ![]() . Ma lo score ha due
. Ma lo score ha due ![]() e quindi un tale
e quindi un tale ![]() non può esistere.
non può esistere.
Per ![]() usiamo il teorema dello score:
usiamo il teorema dello score:
 |
(1).
La risposta è no, dato che qualsiasi grafo ![]() con
con
![]() ha
ha ![]() vertici e
vertici e
![]() lati, quindi per ogni tale
grafo
lati, quindi per ogni tale
grafo
![]() .
.
(2).
La risposta è no, dato che i grafi ![]() -connessi hanno tutti i vertici di grado
almeno
-connessi hanno tutti i vertici di grado
almeno ![]() , ma in ogni garfo
, ma in ogni garfo ![]() con
con
![]() esistono
esistono ![]() vertci di
grado
vertci di
grado ![]() .
.
(3).
Anche in questo caso la risposta è no. Proviamo che se
![]() allora
allora
![]() è connesso. Infatti sia
è connesso. Infatti sia ![]() il vertice di grado
il vertice di grado ![]() . Sia
. Sia ![]() l'unico
vertce non adiacente a
l'unico
vertce non adiacente a ![]() . Per come è fatto
. Per come è fatto ![]() ,
,
![]() , quindi
esiste un vertice
, quindi
esiste un vertice ![]() tale che
tale che
![]() . Ma allora anche
. Ma allora anche
![]() , quindi ogni vertice di
, quindi ogni vertice di ![]() è congiungibile con
è congiungibile con ![]() , da cui
la tesi.
, da cui
la tesi.
![]()
Soluzione dell'esercizio 4 Se per assurdo per ogni ![]() si
avesse che
si
avesse che ![]() è aciclico, allora per il teorema di caratterizzazione degli
alberi,
è aciclico, allora per il teorema di caratterizzazione degli
alberi, ![]() sarebbe un albero, ma allora dovrebbe aversi
sarebbe un albero, ma allora dovrebbe aversi
![]() , e ciò è assurdo.
, e ciò è assurdo.
Osserviamo che se si aggiunge un lato con gli estremi in una stessa componente
connessa di ![]() , allora dato che questa è un albero, per il teorema di
caratterizzazione degli alberi, si ottengono dei cicli. Quindi se si vuole che
il grafo rimanga aciclico, bisogna aggiungere un lato con i vertici su due
diverse componenti connesse.
Proviamo che in tal caso il grafo rimane aciclico. Infatti se ci fosse un ciclo
questo dovrebbe contenere il lato
, allora dato che questa è un albero, per il teorema di
caratterizzazione degli alberi, si ottengono dei cicli. Quindi se si vuole che
il grafo rimanga aciclico, bisogna aggiungere un lato con i vertici su due
diverse componenti connesse.
Proviamo che in tal caso il grafo rimane aciclico. Infatti se ci fosse un ciclo
questo dovrebbe contenere il lato ![]() che si sta aggiungendo. Ma ciò
significa che i due vertici a capo di questo lato dovrebbero essere congiunti da
un cammino in
che si sta aggiungendo. Ma ciò
significa che i due vertici a capo di questo lato dovrebbero essere congiunti da
un cammino in ![]() , ma questo è impossibile perché i due stremi stanno su
componenti connesse di
, ma questo è impossibile perché i due stremi stanno su
componenti connesse di ![]() .
.
Aggiungendo un lato in questo modo si ottiene un nuovo grafo aciclico, con lo
stesso numero di vertici ed un lato in più (e una componente connessa in meno). Si può quindi iterare il
procedimento fino a quando il grafo non risulta connesso, ossia fino a quando il
numero di lati è pari al numero di vertici meno ![]() , ossia per
, ossia per ![]() volte.
volte.
Pertanto il massimo numero di lati che si possono aggiungere a ![]() facendolo
rimanere aciclico è
facendolo
rimanere aciclico è ![]() .
.
![]()