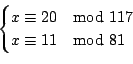Next: Soluzioni proposte
Matematica Discreta (II modulo)
Secondo appello, a.a. 2001/2002
compito 1
Date: 29 giugno 2003
Da svolgersi in tre ore. Al candidato si richiede di svolgere almeno un
esercizio di ciascuno dei due gruppi e di rispondere ad almeno una delle domande
teoriche. Tutte le risposte devono essere
motivate.
Non è ammessa la consultazione di libri e/o appunti.
Esercizio 1
Dire, motivando la risposta, se il seguente sistema di congruenze ammette soluzioni ed in tal
caso determinarle tutte:
Soluzione
Esercizio 3
Sia
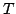
un albero che abbia soltanto vertici di grado
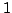
,
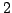
e
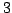
e con esattamente
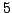
vertici di grado
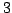
.
- Si provi che
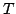 ha esattamente
ha esattamente 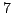 foglie (vertici di grado
foglie (vertici di grado 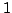 ).
).
- Si disegnino due di questi alberi che non siano isomorfi.
- Si dica, motivando la risposta se l'insieme di tali alberi a
meno di isomorfismo è finito, ed in tal caso determinarne la
cardinalità.
Soluzione
Esercizio 4
Siano
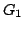
e
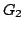
i grafi definiti
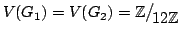
e
- Dire, motivando la risposta se i due grafi sono isomorfi oppure no.
- Determinare
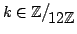 in modo che il grafo
in modo che il grafo 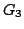 definito da
definito da
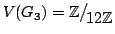 e
e
abbia esattamente 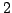 componenti connesse.
componenti connesse.
Soluzione
Domanda di teoria 1.
Dopo aver enunciato il principio di induzione nella seconda forma, si enunci e
si provi il teorema di rappresentazione dei numeri naturali rispetto
ad una base fissata.
Domanda di teoria 2.
Dopo aver definito l'albero di copertura di un grafo, si enunci e si
provi il teorema di esistenza dell'albero di copertura per i grafi finiti.



Next: Soluzioni proposte
Domenico Luminati
2004-07-06