Soluzione dell'esercizio 2 (1). L'insieme
Soluzione dell'esercizio 2 (1). L'insieme
![]() è in
bigezione con l'insieme
è in
bigezione con l'insieme
![]() . Una bigezione è data ad esempio dalla
funzione
. Una bigezione è data ad esempio dalla
funzione
![]() definita da
definita da
(2). L'insieme
![]() è in
bigezione con l'insieme
è in
bigezione con l'insieme
![]() . Una bigezione è data
ad esempio dalla funzione
. Una bigezione è data
ad esempio dalla funzione
![]() definita da
definita da
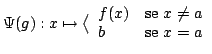
Soluzione dell'esercizio 3 ![]() non può essere lo score di un grafo, dato che contiene un
numero dispari (9) di elementi dispari.
non può essere lo score di un grafo, dato che contiene un
numero dispari (9) di elementi dispari.
![]() è lo score di un grafo, ad esempio se si usa il teorema dello score:
è lo score di un grafo, ad esempio se si usa il teorema dello score:
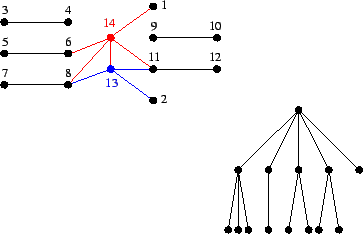 |
(1). La risposta è sì. Basta prendere ad esempio il grafo sulla destra di figura 1.
(2). La risposta è sì. Basta prendere ad esempio il grafo sulla sinistra di figura 1.
(3). La risposta è no, dato che in un grafo 2-connesso non possono esserci vertici di grado 1.
Soluzione dell'esercizio 4 ![]() è hamiltoniano, ad esempio
è hamiltoniano, ad esempio
![]() è un ciclo
hamiltoniano di
è un ciclo
hamiltoniano di ![]() . In particolare
. In particolare ![]() è 2-connesso.
è 2-connesso.
![]() e
e ![]() non sono 2-connessi, dato che
non sono 2-connessi, dato che ![]() e
e ![]() sono isomorfi all'unione disgiunta di due 3-cicli.
Quindi
sono isomorfi all'unione disgiunta di due 3-cicli.
Quindi
![]() e
e
![]() .
.
In ![]() gli unici due vertici di grado
gli unici due vertici di grado ![]() sono congiunti da un lato,
mentre in
sono congiunti da un lato,
mentre in ![]() i due vertici di grado
i due vertici di grado ![]() non sono adiacenti. Quindi
non sono adiacenti. Quindi
![]() .
.
![]()