


Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 1999/2000
Matematica Discreta (II modulo)
Secondo appello, a.a. 1999/2000
10 luglio 2000
Esercizio 1
Si supponga di avere un mazzo con 15 carte e si eseguano le seguenti
operazioni:
- Si dispongano le carte in una matrice
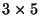 procedendo per colonne
(da sinistra a destra e dall'alto in basso)
procedendo per colonne
(da sinistra a destra e dall'alto in basso)
- si raccolgano le carte procedendo per righe (dall'alto in basso e da
sinistra a destra)
Dire, motivando la risposta, se dopo un numero finito (positivo) di tali
operazioni il mazzo torna nella posizione iniziale. In caso di risposta
affermativa, calcolare il minimo tale numero.
Soluzione
Esercizio 2
Si determini l'insieme delle soluzioni del sistema di congruenze:
Soluzione
Esercizio 3
Sia
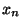
la soluzione dell'equazione ricorsiva lineare
con dati iniziali
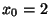
e
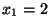
. Si provi che
- Si provi che
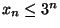 per ogni
per ogni 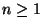 .
.
- Si determini
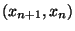 per ogni
per ogni 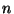 .
.
- Si determini una forma esplicita della soluzione dell'equazione.
Soluzione
Esercizio 4
Siano
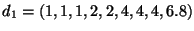
e
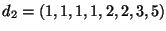
. Dire, motivando
la risposta, per quali
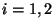
esiste un grafo
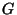
tale che
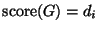
.
In caso di risposta affermativa costruire un tale grafo e dire, motivando la
risposta, se tale score è realizzabile da un albero.
Soluzione
Esercizio 5
Sia
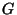
un grafo 2-connesso. Si provi che
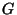
non ha foglie. Dire, motivando
la risposta, se è vero che un grafo finito, connesso, senza foglie e con
almeno tre vertici è necessariamente
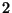
-connesso.
Soluzione



Next: Soluzioni proposte
Previous: Matematica Discreta - II modulo 1999/2000
Luminati Domenico
2002-05-16
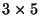 procedendo per colonne
(da sinistra a destra e dall'alto in basso)
procedendo per colonne
(da sinistra a destra e dall'alto in basso)