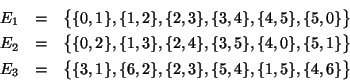

Next: About this document ...
Up: Testo degli esercizi
Previous: Testo degli esercizi
Soluzione dell'esercizio 1 Eseguire le due operazioni produce una permutazione del mazzo di carte e iterare
le due permutazioni corrisponde ad iterare la stessa permutazione. Dato che ogni
permutazione di un insieme finito ha ordine finito (i.e. se 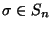 esiste
esiste 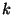 tale che
tale che 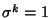 ) allora dopo un numero finito di volte il
mazzo tornerà nella disposizione di partenza.
) allora dopo un numero finito di volte il
mazzo tornerà nella disposizione di partenza.
Per determinare il minimo tale numero scriviamo esplicitamente la
permutazione. La prima operazione sistema le carte nel modo seguente:
raccogliendo quindi per righe le carte si ottiene la permutazione
la cui decomposizione in cicli disgiunti è:
L'ordine di 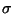 , ossia il minimo intero positivo per cui
, ossia il minimo intero positivo per cui 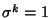 è
dato dal minimo comune multiplo delle lunghezze dei cicli, ossia
è
dato dal minimo comune multiplo delle lunghezze dei cicli, ossia 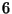 .
.
Soluzione dell'esercizio 2 Dato che
 il sistema è
equivalente a:
il sistema è
equivalente a:
Calcoliamo il massimo comun divisore tra 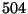 e
e 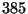 usando l'algoritmo di
Euclide.
usando l'algoritmo di
Euclide.
quindi 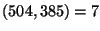 e pertanto il sistema di congruenze ha soluzione (dato che
e pertanto il sistema di congruenze ha soluzione (dato che
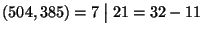 .
Esprimiamo
.
Esprimiamo 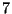 come combinazione intera di
come combinazione intera di 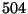 e
e 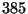 .
.
Quindi,
e per tanto
è una soluzione del sistema.
Dato che il minimo comune multiplo tra 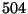 e
e 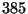 è dato da
è dato da
![$[504,385]=504\cdot 385/(504,385)=504\cdot 385/7=27720$](img47.gif) , l'insieme delle
soluzioni del sistema è:
, l'insieme delle
soluzioni del sistema è:
Soluzione dell'esercizio 3 (1). Procediamo per induzione su 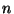 . Per
. Per 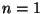 si ha che
si ha che 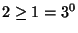 . Supponiamo
. Supponiamo 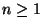 , e che la tesi sia vera per
, e che la tesi sia vera per 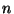 , e proviamo che allora
è vera per
, e proviamo che allora
è vera per 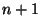 . Infatti
. Infatti
Dove la seconda disuguaglianza è data dall'ipotesi di induzione, mentre la
prima dal fatto che per ogni 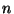 si ha che
si ha che 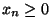 .
.
Quest'ultimo fatto lo proviamo nuovamente per induzione. Per 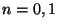 la tesi è
banale. Se
la tesi è
banale. Se 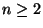 allora
allora
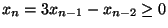 in quanto per ipotesi di
induzione
in quanto per ipotesi di
induzione 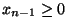 e
e 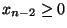 .
.
(2). Proviamo che
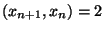 per ogni
per ogni 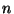 . Per
. Per 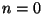 la tesi
è banale. Supponiamo la tesi vera per
la tesi
è banale. Supponiamo la tesi vera per 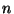 e proviamola per
e proviamola per 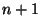 . Dalla
relazione
. Dalla
relazione
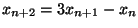 e dal lemma per la dimostrazione dell'algoritmo
di Euclide, segue che
e dal lemma per la dimostrazione dell'algoritmo
di Euclide, segue che
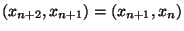 e quest'ultimo, per
ipotesi di induzione è
e quest'ultimo, per
ipotesi di induzione è 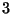 .
.
(3). Il polinomio caratteristico dell'equazione è dato da 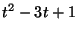 le cui radici sono
le cui radici sono
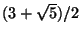 e
e
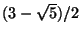 . La soluzione generale
dell'equazione ricorsiva è allora data da:
. La soluzione generale
dell'equazione ricorsiva è allora data da:
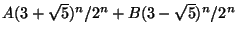 . Imponendo le due condizioni
iniziali si ottiene il sistema:
. Imponendo le due condizioni
iniziali si ottiene il sistema:
le cui soluzioni sono
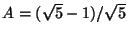 e
e
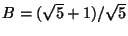 ,
quindi la successione definita per ricorrenza è data da:
,
quindi la successione definita per ricorrenza è data da:
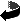
Soluzione dell'esercizio 4 Osserviamo che in 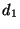 compaiono tre numeri dispari, quindi non può essere lo
score di un grafo dato che in tal caso il numero di numeri dispari dovrebbe
essere pari.
compaiono tre numeri dispari, quindi non può essere lo
score di un grafo dato che in tal caso il numero di numeri dispari dovrebbe
essere pari.
Usiamo il teorema dello score per determinare se 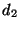 è realizzabile oppure
no.
è realizzabile oppure
no.
Evidentemente 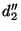 è realizzabile e pertanto
è realizzabile e pertanto 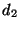 lo è (vedi la figura
lo è (vedi la figura
![[*]](crossref.png) ).
).
Figura 1:
Un grafo che realizza 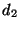 come score (esercizio 4)
come score (esercizio 4)
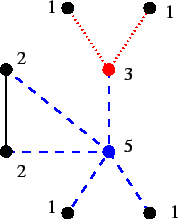 |
Osserviamo
inoltre che 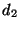 non può essere realizzato da un albero in quanto se
non può essere realizzato da un albero in quanto se 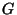 è
un grafo che realizza
è
un grafo che realizza 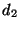 allora
allora
Un tale grafo non può quindi essere un albero in quanto se lo fosse si avrebbe
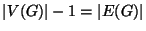 .
.
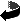
Soluzione dell'esercizio 5 Per assurdo sia 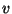 una foglia di
una foglia di 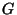 e sia
e sia 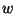 l'unico vertice tale che
l'unico vertice tale che
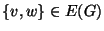 . Allora in
. Allora in 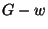 non ci sono lati che partono da
non ci sono lati che partono da 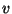 , ma ci
sono altri vertici diversi da
, ma ci
sono altri vertici diversi da 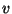 (essendo
(essendo 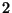 -connesso,
-connesso, 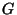 ha almeno
ha almeno 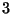 vertici), quindi
vertici), quindi 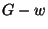 è sconnesso. Assurdo.
è sconnesso. Assurdo.
Il viceversa non è vero, si consideri ad esempio il grafo 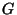 rappresentato in
figura 2.
rappresentato in
figura 2.
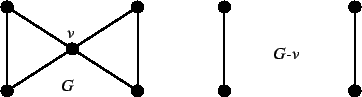
Figura 2:
Il contresempio dell'esercizio 5, G è connesso, non ha foglie ma
non è 2-connesso
 |
Il grafo 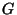 non ha foglie, è connesso ed ha più di 3 vertici ma non è nemmeno
non ha foglie, è connesso ed ha più di 3 vertici ma non è nemmeno 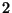 -connesso.
-connesso.
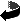
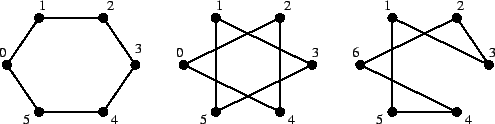
Soluzione dell'esercizio 6 Scriviamo esplicitamente i lati dei tre grafi:
Figura 3:
I gragfi 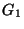 e
e 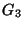 sono dei cicli, mente il grafo
sono dei cicli, mente il grafo  è costituito da due cicli disgiunti, in particolare non è connesso
è costituito da due cicli disgiunti, in particolare non è connesso
 |
Osserviamo che
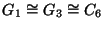 , dato che
, dato che
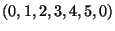 è un ciclo in
è un ciclo in
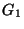 che contiene tutti i vertici e tutti i lati e anche
che contiene tutti i vertici e tutti i lati e anche
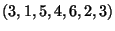 è
un ciclo in
è
un ciclo in 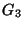 che contiene tutti i vertici e tutti i lati. In particolare
che contiene tutti i vertici e tutti i lati. In particolare
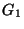 e
e 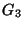 sono connessi. Il grafo
sono connessi. Il grafo 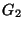 non è connesso, in quanto è
costituito dai due cicli
non è connesso, in quanto è
costituito dai due cicli 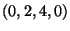 e
e 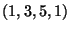 che non hanno vertici in
comune. Quindi
che non hanno vertici in
comune. Quindi 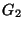 non è isomorfo né a
non è isomorfo né a 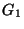 né a
né a 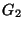 . Si veda la
figura3.
. Si veda la
figura3.
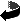


Next: About this document ...
Up: Testo degli esercizi
Previous: Testo degli esercizi
Luminati Domenico
2002-05-16


![]() il sistema è
equivalente a:
il sistema è
equivalente a:
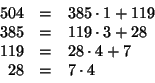
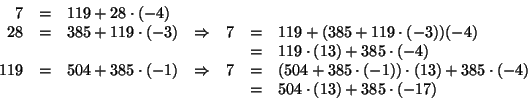
![]() . Per
. Per ![]() si ha che
si ha che ![]() . Supponiamo
. Supponiamo ![]() , e che la tesi sia vera per
, e che la tesi sia vera per ![]() , e proviamo che allora
è vera per
, e proviamo che allora
è vera per ![]() . Infatti
. Infatti
![]() la tesi è
banale. Se
la tesi è
banale. Se ![]() allora
allora
![]() in quanto per ipotesi di
induzione
in quanto per ipotesi di
induzione ![]() e
e ![]() .
.
![]() per ogni
per ogni ![]() . Per
. Per ![]() la tesi
è banale. Supponiamo la tesi vera per
la tesi
è banale. Supponiamo la tesi vera per ![]() e proviamola per
e proviamola per ![]() . Dalla
relazione
. Dalla
relazione
![]() e dal lemma per la dimostrazione dell'algoritmo
di Euclide, segue che
e dal lemma per la dimostrazione dell'algoritmo
di Euclide, segue che
![]() e quest'ultimo, per
ipotesi di induzione è
e quest'ultimo, per
ipotesi di induzione è ![]() .
.
![]() le cui radici sono
le cui radici sono
![]() e
e
![]() . La soluzione generale
dell'equazione ricorsiva è allora data da:
. La soluzione generale
dell'equazione ricorsiva è allora data da:
![]() . Imponendo le due condizioni
iniziali si ottiene il sistema:
. Imponendo le due condizioni
iniziali si ottiene il sistema:
![]() compaiono tre numeri dispari, quindi non può essere lo
score di un grafo dato che in tal caso il numero di numeri dispari dovrebbe
essere pari.
compaiono tre numeri dispari, quindi non può essere lo
score di un grafo dato che in tal caso il numero di numeri dispari dovrebbe
essere pari.
![]() è realizzabile oppure
no.
è realizzabile oppure
no.
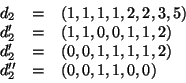
![[*]](crossref.png) ).
Osserviamo
inoltre che
).
Osserviamo
inoltre che 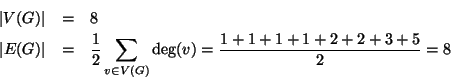
![]() una foglia di
una foglia di ![]() e sia
e sia ![]() l'unico vertice tale che
l'unico vertice tale che
![]() . Allora in
. Allora in ![]() non ci sono lati che partono da
non ci sono lati che partono da ![]() , ma ci
sono altri vertici diversi da
, ma ci
sono altri vertici diversi da ![]() (essendo
(essendo ![]() -connesso,
-connesso, ![]() ha almeno
ha almeno ![]() vertici), quindi
vertici), quindi ![]() è sconnesso. Assurdo.
è sconnesso. Assurdo.
![]() rappresentato in
figura 2.
rappresentato in
figura 2.