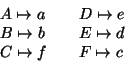![]() , quindi
, quindi ![]() e quindi
e quindi
![]() ovvero
ovvero
![]() . Ovvero
. Ovvero
![]() .
.
Utilizzando il piccolo teorema di Fermat, si ottiene allora:
Soluzione dell'esercizio 2 Il polinomio caratteristico è dato da ![]() le cui radici sono
le cui radici sono
![]() e
e ![]() , quindi una base dello spazio delle soluzioni è
data dalle due successioni
, quindi una base dello spazio delle soluzioni è
data dalle due successioni
![]() e
e
![]() , quindi
la soluzione generale dell'equazione è data da:
, quindi
la soluzione generale dell'equazione è data da:
Soluzione dell'esercizio 3 (1).
![]() , se e solo se
, se e solo se
![]() e
e
![]() , possiamo quindi definire l'applicazione
, possiamo quindi definire l'applicazione
![]() ponendo
ponendo
![]() è suriettiva. Infatti se
è suriettiva. Infatti se ![]() e
e ![]() , allora è ben
definita la funzione
, allora è ben
definita la funzione ![]() ponendo
ponendo
Ma allora ![]() è una bigezione, e quindi:
è una bigezione, e quindi:
(2). Dati due insiemi ![]() e
e ![]() indichiamo con
indichiamo con ![]() l'insieme delle
applicazioni iniettive
l'insieme delle
applicazioni iniettive ![]() . Sappiamo che se
. Sappiamo che se ![]() e
e ![]() sono finiti, allora
sono finiti, allora
![]() .
.
Osserviamo che se
![]() se e solo se
se e solo se
![]() e
e
![]() . Quindi è ben definita
l'applicazione
. Quindi è ben definita
l'applicazione
![]() ponendo
ponendo
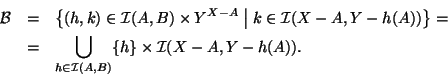

Soluzione dell'esercizio 4 Usiamo il teorema dello score.

Per provare che ogni grafo ![]() tale che
tale che
![]() è euleriano, basta
provare che ogni tale grafo è connesso. In tal cao infatti, dato che tutti i
verici hanno grado pari, il teorema di caratterizzazione dei grafi euleriani
garantisce la tesi.
è euleriano, basta
provare che ogni tale grafo è connesso. In tal cao infatti, dato che tutti i
verici hanno grado pari, il teorema di caratterizzazione dei grafi euleriani
garantisce la tesi.
Siano ![]() un vertice di grado
un vertice di grado ![]() e siano
e siano ![]() i vertici a lui
adiacenti (i.e.
i vertici a lui
adiacenti (i.e.
![]() per
per ![]() ). Sia
). Sia ![]() il vertice
rimanente, allora, dato che
il vertice
rimanente, allora, dato che ![]() , esiste
, esiste ![]() tale che
tale che
![]() , pertanto
, pertanto ![]() è un cammino che collega
è un cammino che collega ![]() a
a ![]() . Ogni
vertice è quindi collegabile al vertice
. Ogni
vertice è quindi collegabile al vertice ![]() e pertanto il grafo è
connesso.
e pertanto il grafo è
connesso.
![]()
Soluzione dell'esercizio 5 Dato che ![]() ha almeno due vertici,
ha almeno due vertici, ![]() ne ha almeno
ne ha almeno ![]() . Osserviamo che
. Osserviamo che
![]() e quindi è connesso. Se invece
e quindi è connesso. Se invece ![]() allora
allora
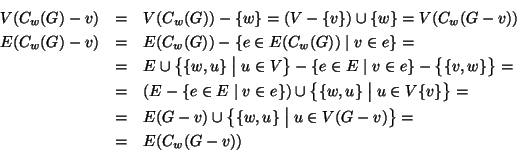
Soluzione dell'esercizio 6 ![]() e
e ![]() sono isomorfi. Un isomorfismo è dato ad esempio da:
sono isomorfi. Un isomorfismo è dato ad esempio da: