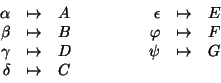

Next: About this document ...
Up: Testo degli esercizi
Previous: Testo degli esercizi
Soluzione dell'esercizio 1
Soluzione dell'esercizio 2 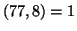 , quindi
, quindi 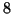 è invertibile modulo
è invertibile modulo 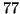 , per tanto la soluzione, se
esiste, è un elemento invertibile. Inoltre
, per tanto la soluzione, se
esiste, è un elemento invertibile. Inoltre
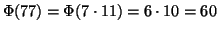 , quindi
, quindi
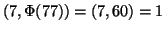 pertanto esiste
pertanto esiste 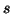 tale che
tale che
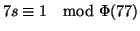 . Per il piccolo teorema di
Fermat,
. Per il piccolo teorema di
Fermat,
![$\left[8^x\right]_{77}$](img35.gif) è allora la soluzione della congruenza.
è allora la soluzione della congruenza.
Usando l'algoritmo di Euclide, si ottiene
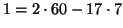 , e quindi la
soluzione è data da
, e quindi la
soluzione è data da
![$\left[8^43\right]_{77}=\left[50\right]_{77}$](img37.gif) .
.
Soluzione dell'esercizio 3
Soluzione dell'esercizio 4
Soluzione dell'esercizio 5 Usiamo il teorema dello score:
Dato che 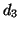 è realizzabile come score di un grafo, anche
è realizzabile come score di un grafo, anche 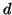 lo è. La
costruzione standard, condotta con un po' di attenzione, produce il grafo in
figura, che è anche connesso e
lo è. La
costruzione standard, condotta con un po' di attenzione, produce il grafo in
figura, che è anche connesso e
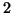 -connesso.
-connesso.
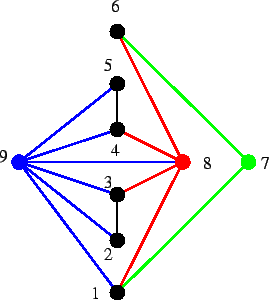
Figura 1:
Il grafo costruito della soluzione dell'esercizio 5. La
configurazione di partenza è data dai vertici 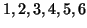 , e dai due
lati
, e dai due
lati
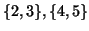 che realizzano lo score
che realizzano lo score 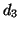 a cui sono
successivamente aggiunti i vertici
a cui sono
successivamente aggiunti i vertici 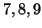 ottenendo dei grafi, che
realizzano, nell'ordine, gli score
ottenendo dei grafi, che
realizzano, nell'ordine, gli score 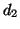 ,
, 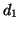 e infine
e infine 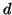
 |
Che il grafo sia  -connesso lo si può vedere mostrando che è ottenuto da
un ciclo con successive aggiunzioni e suddivisioni di lati
(cfr. figura).
-connesso lo si può vedere mostrando che è ottenuto da
un ciclo con successive aggiunzioni e suddivisioni di lati
(cfr. figura).
Figura 2:
Il grafo della soluzione dell'esercizio 5 è 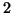 -connesso
-connesso
 |
Soluzione dell'esercizio 6 Il primo grafo è hamiltoniano (in particolare quindi è 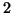 -connesso) in
quanto c'è il ciclo
-connesso) in
quanto c'è il ciclo
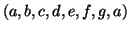 .
.
Il terzo grafo non è 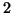 -connesso, infatti se a questo grafo si toglie il
vertice
-connesso, infatti se a questo grafo si toglie il
vertice 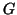 si ottengono i due cicli
si ottengono i due cicli 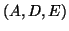 e
e 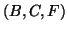 .
.
Il secondo e il terzo grafo sono isomorfi(quindi il primo e il secondo non lo
sono). Un isomorfismo è dato ad esempio dalla funzione definita da:
Che tale funzione sia un isomorfismo segue dal fatto che il vertice 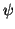 e la
sua immagine
e la
sua immagine 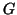 sono collegati con tutti gli altri vertici. I vertici
sono collegati con tutti gli altri vertici. I vertici
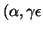 oltre a essere collegati con
oltre a essere collegati con 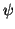 sono collegati
soltanto tra loro in tutti i modi possibili e anche le rispettive immagini
sono collegati
soltanto tra loro in tutti i modi possibili e anche le rispettive immagini
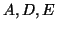 sono collegati solo tra loro (in tutti i modo possibili) oltre che con
sono collegati solo tra loro (in tutti i modo possibili) oltre che con
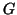 . Anche l'altra terna di vertici
. Anche l'altra terna di vertici
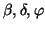 e le rispettive immagini
e le rispettive immagini
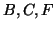 hanno la stessa proprietà, quindi i lati di un grafo sono messi in
bigezione con i lati dell'altro.
hanno la stessa proprietà, quindi i lati di un grafo sono messi in
bigezione con i lati dell'altro.


Next: About this document ...
Up: Testo degli esercizi
Previous: Testo degli esercizi
Luminati Domenico
2002-05-16
![]() , quindi
, quindi ![]() è invertibile modulo
è invertibile modulo ![]() , per tanto la soluzione, se
esiste, è un elemento invertibile. Inoltre
, per tanto la soluzione, se
esiste, è un elemento invertibile. Inoltre
![]() , quindi
, quindi
![]() pertanto esiste
pertanto esiste ![]() tale che
tale che
![]() . Per il piccolo teorema di
Fermat,
. Per il piccolo teorema di
Fermat,
![]() è allora la soluzione della congruenza.
è allora la soluzione della congruenza.
![]() , e quindi la
soluzione è data da
, e quindi la
soluzione è data da
![]() .
.
![]()
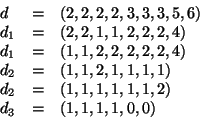

![]() -connesso) in
quanto c'è il ciclo
-connesso) in
quanto c'è il ciclo
![]() .
.
![]() -connesso, infatti se a questo grafo si toglie il
vertice
-connesso, infatti se a questo grafo si toglie il
vertice ![]() si ottengono i due cicli
si ottengono i due cicli ![]() e
e ![]() .
.