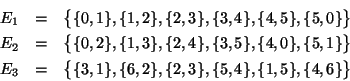

Next: About this document ...
Up: Testo degli esercizi
Previous: Testo degli esercizi
Soluzione dell'esercizio 1
Soluzione dell'esercizio 2 (1).
(2). Dato che
![$[x_{n},x_{n+1}]=x_{n}x_{n+1}/(x_{n},x_{n+1})$](img23.gif) ,
provare la tesi equivale a provare che
,
provare la tesi equivale a provare che
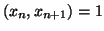 per ogni
per ogni 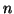 . Lo
facciamo per induzione su
. Lo
facciamo per induzione su 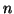 . Se
. Se 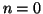 ,
,
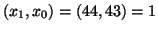 , dato che sono
numeri consecutivi. Supponiamo la
tesi vera per
, dato che sono
numeri consecutivi. Supponiamo la
tesi vera per 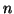 e proviamola per
e proviamola per 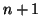 . Dalla relazione di ricorrenza si ha
che
. Dalla relazione di ricorrenza si ha
che
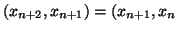 e per ipotesi di
induzione, quest'ultimo è
e per ipotesi di
induzione, quest'ultimo è 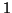 .
.
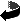
Soluzione dell'esercizio 3
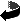
Soluzione dell'esercizio 4
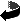
Soluzione dell'esercizio 5
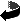
Soluzione dell'esercizio 6 Scriviamo esplicitamente i lati dei tre grafi:
Figura 1:
I gragfi 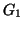 e
e 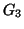 sono dei cicli, mente il grafo
sono dei cicli, mente il grafo 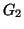 è costituito da due cicli disgiunti, in particolare non è connesso
è costituito da due cicli disgiunti, in particolare non è connesso
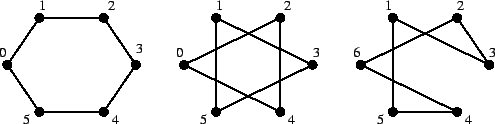 |
Osserviamo che
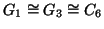 , dato che
, dato che
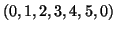 è un ciclo in
è un ciclo in
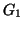 che contiene tutti i vertici e tutti i lati e anche
che contiene tutti i vertici e tutti i lati e anche
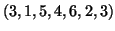 è
un ciclo in
è
un ciclo in 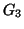 che contiene tutti i vertici e tutti i lati. In particolare
che contiene tutti i vertici e tutti i lati. In particolare
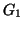 e
e 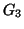 sono connessi. Il grafo
sono connessi. Il grafo 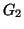 non è connesso, in quanto è
costituito dai due cicli
non è connesso, in quanto è
costituito dai due cicli 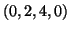 e
e 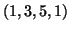 che non hanno vertici in
comune. Quindi
che non hanno vertici in
comune. Quindi 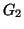 non è isomorfo né a
non è isomorfo né a 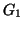 né a
né a 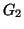 . Si veda la
figura1.
. Si veda la
figura1.


Next: About this document ...
Up: Testo degli esercizi
Previous: Testo degli esercizi
Luminati Domenico
2002-05-16
![]() ,
provare la tesi equivale a provare che
,
provare la tesi equivale a provare che
![]() per ogni
per ogni ![]() . Lo
facciamo per induzione su
. Lo
facciamo per induzione su ![]() . Se
. Se ![]() ,
,
![]() , dato che sono
numeri consecutivi. Supponiamo la
tesi vera per
, dato che sono
numeri consecutivi. Supponiamo la
tesi vera per ![]() e proviamola per
e proviamola per ![]() . Dalla relazione di ricorrenza si ha
che
. Dalla relazione di ricorrenza si ha
che
![]() e per ipotesi di
induzione, quest'ultimo è
e per ipotesi di
induzione, quest'ultimo è ![]() .
.
![]()