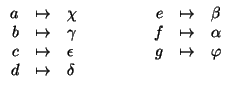L'insieme delle soluzioni è allora dato da
![]()
![]()
Soluzione dell'esercizio 2 (1). Se
![]() e
e
![]() allora l'insieme delle funzioni iniettive da
allora l'insieme delle funzioni iniettive da
![]() in
in ![]() ha cardinalità
ha cardinalità
![]() . Nel nostro
caso
. Nel nostro
caso ![]() ,
, ![]() , quindi
, quindi
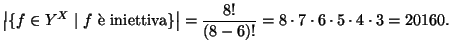
(2).
Se consideriamo
![]() e
e
![]() alora l'insieme
alora l'insieme
![]() è iniettiva e
è iniettiva e ![]() può essere messo in
bigezione con l'insieme
può essere messo in
bigezione con l'insieme
![]() è iniettiva
è iniettiva![]() mediante la restrizione. Ma allora, applicando la stessaa formula del punto
precedente, si ottiene che la cardinalità cercate è pari a
mediante la restrizione. Ma allora, applicando la stessaa formula del punto
precedente, si ottiene che la cardinalità cercate è pari a
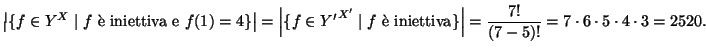
(3).
Dato che ![]() è iniettiva,
è iniettiva,
![]() . D'altra parte, dato che
. D'altra parte, dato che
![]() , possono
essere assunti tutti i tre valori
, possono
essere assunti tutti i tre valori ![]() . Costruiamo degli esempi:
. Costruiamo degli esempi:
Soluzione dell'esercizio 3 Un grafo ![]() tale che
tale che
![]() dovrebbe avere
dovrebbe avere ![]() vertici, due vertici,
chiamiamoli
vertici, due vertici,
chiamiamoli ![]() e
e ![]() ,
di grado
,
di grado ![]() , ossia adiacenti a tutti gli altri. Ma allora ogni vertice diverso
da
, ossia adiacenti a tutti gli altri. Ma allora ogni vertice diverso
da ![]() e
e ![]() questi due deve essere adiacente almeno ad uno di loro e quindi avere grado
almeno
questi due deve essere adiacente almeno ad uno di loro e quindi avere grado
almeno ![]() . Ma se
. Ma se
![]() esiste almeno un vertce di grado
esiste almeno un vertce di grado ![]() , che è
in contraddizione con quanto appena provato. Quindi un tale
, che è
in contraddizione con quanto appena provato. Quindi un tale ![]() non può
esistere.
non può
esistere.
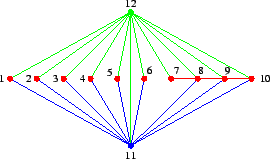
Per ![]() usiamo il teorema dello score:
usiamo il teorema dello score:
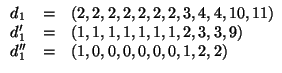
 |
(1).
La risposta è no. Se ![]() è un grafo tale che
è un grafo tale che
![]() allora
allora
![]() e
e
![]() . Ma allora
. Ma allora
![]() , quindi
, quindi ![]() non può essere un albero.
non può essere un albero.
(2).
La risposta è no. Se ![]() è un grafo tale che
è un grafo tale che
![]() allora
esiste
allora
esiste ![]() tale che
tale che
![]() , ossia ogni altro vertice è adiacente e
quindi congiungibile con
, ossia ogni altro vertice è adiacente e
quindi congiungibile con ![]() . Ne consegue che
. Ne consegue che ![]() è connesso.
è connesso.
(3).
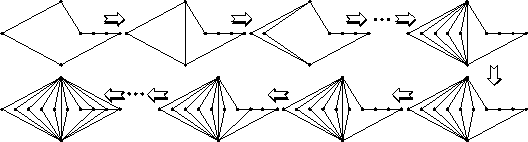
Che il grafo di figura 1 sia ![]() -connesso lo si può
vedere mostrando che è ottenuto da un ciclo con successive aggiunzioni e
suddivisioni di lati (cfr. figura).
-connesso lo si può
vedere mostrando che è ottenuto da un ciclo con successive aggiunzioni e
suddivisioni di lati (cfr. figura).
 |
Un altro modo di provare la ![]() -connessione di questo grafo è il seguente. Sia
-connessione di questo grafo è il seguente. Sia
![]() il grafo e sia
il grafo e sia![]() il vertice di grado
il vertice di grado ![]() . Chiaramente, per ogni
. Chiaramente, per ogni ![]() si ha che
si ha che ![]() ha
un vertice di grado
ha
un vertice di grado ![]() (e
(e ![]() vertici) e quindi è connesso. D'altra parte
vertici) e quindi è connesso. D'altra parte
![]() ha anche un vertice
ha anche un vertice ![]() di grado
di grado ![]() e quindi
e quindi ![]() ha grado
ha grado ![]() in
in ![]() (è adiacente a tutti i suoi vertici tranne uno) e dato che ogni vertice di
(è adiacente a tutti i suoi vertici tranne uno) e dato che ogni vertice di ![]() ha
grado almeno
ha
grado almeno ![]() , ogni vertice di
, ogni vertice di ![]() ha grado almeno
ha grado almeno ![]() . Ma allora l'unico
vertice
. Ma allora l'unico
vertice ![]() di
di ![]() non adiacente a
non adiacente a ![]() sarà adiacente almeno ad un altro vertice
sarà adiacente almeno ad un altro vertice ![]() e
quindi
e
quindi ![]() è un cammino tra
è un cammino tra ![]() e
e ![]() in
in ![]() . Ne consegue che tutti i vertici
di
. Ne consegue che tutti i vertici
di ![]() sono congiungibili a
sono congiungibili a ![]() e quindi anche
e quindi anche ![]() è connesso. Questo
ragionamento prova in realtà che ogni grafo tale che
è connesso. Questo
ragionamento prova in realtà che ogni grafo tale che
![]() è
è ![]() -connesso.
-connesso.
![]()
Soluzione dell'esercizio 4 Il primo grafo non è ![]() -connesso, infatti se a questo grafo si toglie il
vertice
-connesso, infatti se a questo grafo si toglie il
vertice ![]() si ottengono i due cicli disgiunti
si ottengono i due cicli disgiunti ![]() e
e ![]() ,
mentre il secondo grafo è hamiltoniano (e quindi quindi è
,
mentre il secondo grafo è hamiltoniano (e quindi quindi è ![]() -connesso) in
quanto c'è il ciclo
-connesso) in
quanto c'è il ciclo
![]() .
.
Di conseguenza il primo ed il secondo grafo non sono isomorfi.
Il secondo e il terzo grafo sono isomorfi (conseguentemente il primo e il terzo
non lo sono). Un isomorfismo è dato ad esempio dalla funzione ![]() definita da:
definita da: