Next: About this document ... Up: Matematica Discreta (II modulo) Previous: Matematica Discreta (II modulo)

Soluzioni proposte

Soluzione dell'esercizio 1

ossia

è invertibile modulo

. Inoltre $\Phi(38)=\Phi(2\cdot19)=1\cdot18=18$ , e

quindi la congruenza ha soluzione unica $\quad{\rm mod}\ 38$ . Determiniamo un inverso positivo di

modulo

$\displaystyle 18$	$\displaystyle =$	$\displaystyle 11 + 7$
$\displaystyle 11$	$\displaystyle =$	$\displaystyle 7 + 4$
$\displaystyle 7$	$\displaystyle =$	$\displaystyle 4 + 3$
$\displaystyle 4$	$\displaystyle =$	$\displaystyle 3 + 1$

da cui

$\displaystyle 1 = 4 - 3 = 4 - ( 7 - 4 ) = 2\cdot 4 -7 = 2(11-7) - 7 = 2\cdot 11 -3\cdot 7 = 2 \cdot 11 -3(18 - 11) = 5 \cdot 11 - 3 \cdot 18.$

Quindi

è un inverso positivo di

modulo

, pertanto la congruenza è equivalente a $x\cong 35^5\quad{\rm mod}\ 38$ e quindi le soluzioni intere sono date da $\left[35^5\right]_{38}=\left[(-3)^5\right]_{38}=\left[(-3)^3\right]_{38}\left[... ...eft[11\right]_{38}\left[9\right]_{38}=\left[99\right]_{38}=\left[23\right]_{23}$ . Dato che $0\le 23 < 38$ ,

è la più piccola soluzione intera.

Soluzione dell'esercizio 2 (1). L'insieme ${\cal P}_1$ è in bigezione con $2^{X\setminus Y}$ , una bigezione essendo data da $\Phi_1:{\cal P}_1\to 2^{X\setminus Y}$ definita ponendo $\Phi_1(A)= A\setminus Y$ . Ma allora

$\displaystyle \left\vert{\cal P}_1\right\vert=\left\vert 2^{X\setminus Y}\right... ...ght\vert}=2^{\left\vert X\right\vert-\left\vert Y\right\vert}= 2^{9-4}=2^5=32.$

(2). ${\cal P}_2$ è in bigezione con ${Y \choose 2}\times (X\setminus Y)$ , una bigezione è data da $\Phi_2:{\cal P}_2\to{Y \choose 2}\times 2^{X\setminus Y}$ definita ponendo $\Phi_2(A)=\big(A\cap Y, A\cap(X\setminus Y)\big)$ . Ma allora

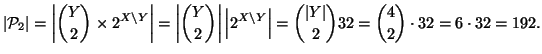
$\displaystyle \left\vert{\cal P}_2\right\vert=\left\vert{Y \choose 2}\times 2^{... ...left\vert Y\right\vert \choose 2}32 ={4 \choose 2} \cdot 32 = 6\cdot 32 = 192.$

(3). ${\cal P}_3=2^X\setminus 2^{X\setminus Y}$ , infatti $A\cap Y\ne\varnothing$ equivale a dire che $A\not\subseteq X\setminus Y$ . Ma allora

$\displaystyle \left\vert{\cal P}_3\right\vert= \left\vert 2^X\setminus 2^{X\set... ...2^{\left\vert X\setminus Y\right\vert}= 2^9-2^5 = 2^5(2^4-1)=32\cdot 15 = 480.$

Soluzione dell'esercizio 3 Un grafo tale che $\mathop{\rm score}\nolimits (G)=d_1$ dovrebbe avere vertici di grado dispiri, ma sappiamo che in ogni grafo il numero di vertici di grado dispari è pari, quindi un tale non può esistere.

Per usiamo il teorema dello score:

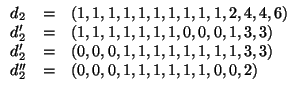
$\displaystyle \begin{array}{lcl} d_2 & = & (1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 , 1 ,... ...3) \\ d_2'' & = & (0 , 0 , 0 , 1 , 1 , 1 , 1 , 1 , 1 , 0 , 0 , 2) \end{array}$

Dato che

è realizzabile come score di un grafo, anche

lo è. La costruzione standard produce il grafo in figura.

**Figura:** Il grafo costruito per la soluzione dell'esercizio 3. La configurazione di partenza è data dai vertici , e dai lati $\{6,7\},\{7,8\},\{9,10\},\{11,12\}$ che realizza a cui sono successivamente aggiunti i vertici ottenendo dei grafi, che realizzano, nell'ordine, e .
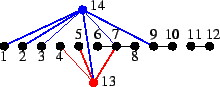$\begin{figure}\begin{center} \psfig{file=fig_a2_1_e31_2001.eps,width=.4\hsize} \end{center}\end{figure}$

(1). La risposta è si. Con un po' di attenzione si può costruire il grafo di figura, che è un albero.

**Figura:** Un albero che realizza lo score dell'esercizio 3.
$\begin{figure}\begin{center} \psfig{file=fig_a2_1_e32_2001.eps,width=7cm} \end{center}\end{figure}$

(2). La risposta è sì. Il grafo costruito in figura è evidentemente sconnesso.

(3). Un tale grafo non potrà certamente essere -connesso dato che contiene necessariamente dei vertici di grado , e sappiamo che ciò è impossibile nei grafi -connessi.

Soluzione dell'esercizio 4 non è -connesso, infatti se glio si toglie il vertice si ottengono i due cicli disgiunti e .

Il grafo è hamiltoniano (e quindi quindi è -connesso) in quanto c'è il ciclo che contiene tutti i vertici.

Anche il grafo è hamiltoniano (e quindi quindi è -connesso) in quanto c'è il ciclo $(\alpha,\delta,\epsilon,\varphi ,\gamma,\eta,\lambda,\beta,\chi,\alpha)$ .

Di conseguenza il primo ed il secondo grafo non sono isomorfi $G_1\not\oldcong G_3$ e $G_2\not\oldcong G_3$ .

Neanche e sono isomorfi, infatti in c'è un vertice $\beta$ che ha grado ed i vertici a lui adiacenti $\chi$ e $\lambda$ hanno entrambi grado . Se ci fosse un isomorfismo $f:G_1\to G_2$ dovrebbe esserci un vertice $f(\beta)$ in con le stesse proprietà, ma i quattro vertici di che hanno grado sono adiacenti ciascuno ad al più un vertice di grado , più esplicitamente: