Soluzione dell'esercizio 2 (1). Indichiamo con rispettivamente con ![]() ,
, ![]() ,
, ![]() ,
, ![]() gli insiemi
dei sassoffonisti, trombettisti, percussionisti e chitarristi che si
presentano alla selezione. Si ha
gli insiemi
dei sassoffonisti, trombettisti, percussionisti e chitarristi che si
presentano alla selezione. Si ha
![]() ,
,
![]() ,
,
![]() ,
,
![]() . Da ciascuno di questi insiemi devono
essere scelti rispettivamente, 5, 3, 2, 2 elementi, quindi l'insieme
. Da ciascuno di questi insiemi devono
essere scelti rispettivamente, 5, 3, 2, 2 elementi, quindi l'insieme
![]() delle possibili band è in bigezione con l'insieme
delle possibili band è in bigezione con l'insieme
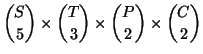
(2).
Il numero di possibili
scelte della cantante è evidentemente ![]() , e quindi il numero delle
[possibili band viene moltiplicato per 4, e diventa 235200.
, e quindi il numero delle
[possibili band viene moltiplicato per 4, e diventa 235200.
(3).
Detti ora ![]() ,
, ![]() ,
, ![]() gli insiemi dei sassofonisti, dei chitarristi
e dei percussionisti della band, l'insieme
gli insiemi dei sassofonisti, dei chitarristi
e dei percussionisti della band, l'insieme
![]() dei possibili
trii è allora in
bigezione con l'insieme
dei possibili
trii è allora in
bigezione con l'insieme
![]() e quindi ha cardinalità
pari a
e quindi ha cardinalità
pari a
Soluzione dell'esercizio 3 Un grafo ![]() tale che
tale che
![]() dovrebbe avere
dovrebbe avere ![]() vertici, di
cui due di grado
vertici, di
cui due di grado ![]() , ossia adiacenti a tutti gli altri. Ma allora
ogni vertice dovrebbe avere grado almeno
, ossia adiacenti a tutti gli altri. Ma allora
ogni vertice dovrebbe avere grado almeno ![]() . Questo cotraddice il
fatto che dovrebbero esserci anche due vertici di grado
. Questo cotraddice il
fatto che dovrebbero esserci anche due vertici di grado ![]() .
.
Per ![]() usiamo il teorema dello score:
usiamo il teorema dello score:

 |
(1).
La risposta è no. Se ![]() è un grafo tale che
è un grafo tale che
![]() allora
allora
![]() e
e
![]() . Ma allora
. Ma allora
![]() , quindi
, quindi ![]() non può essere un albero.
non può essere un albero.
(2).
La risposta è sì. Basta prendere il grafo che si è costruito in
precedenza. In realtà si può
mostrare che ogni tale grafo è necessariamente connesso, dato che ha
![]() vertici, un vertice di grado
vertici, un vertice di grado ![]() e quindi adiacente ad ogni altro
vertice tranne uno, e quest'ultimo vertice avendo grado positivo,
sarà necessariamente adiacente ad uno dei precedenti.
e quindi adiacente ad ogni altro
vertice tranne uno, e quest'ultimo vertice avendo grado positivo,
sarà necessariamente adiacente ad uno dei precedenti.
(3).
La risposta è no. Se ![]() è un grafo tale che
è un grafo tale che
![]() allora ha un vertice di grado
allora ha un vertice di grado ![]() , quindi non può essere
, quindi non può essere ![]() -connesso.
-connesso.
![]()
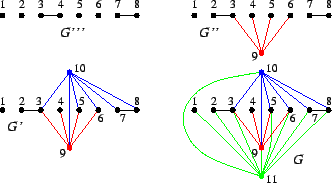
Soluzione dell'esercizio 4 Tutti i grafi hanno un unico vertice di grado massimo (in tutti e tre
i casi è il vertice ![]() ),
), ![]() e quindi
sono isomorfi se e solo se lo sono privati di questo vertice. Questo
perchè se
e quindi
sono isomorfi se e solo se lo sono privati di questo vertice. Questo
perchè se ![]() ha grado massimo in
ha grado massimo in ![]() allora
allora ![]() è ottenuto da
è ottenuto da
![]() aggiungendo un vertice collegato con tutti gli altri lati.
aggiungendo un vertice collegato con tutti gli altri lati.
Ma ora ![]() è costituito dall'unione disgiunta di tre copie di
è costituito dall'unione disgiunta di tre copie di
![]() (ha quindi 3 componenti connesse), mentre
(ha quindi 3 componenti connesse), mentre ![]() e
e ![]() sono
entrambi costituiti dall'unione disgiunta di un
sono
entrambi costituiti dall'unione disgiunta di un ![]() e un
e un ![]() (in
particolare hanno due componenti connesse). Quindi
(in
particolare hanno due componenti connesse). Quindi
![]() ,
mentre
,
mentre
![]() e
e
![]() . Un isomorfismo
. Un isomorfismo
![]() è dato ad esempio da:
è dato ad esempio da: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() e
e ![]() .
.
![]()