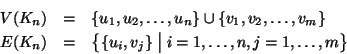Next: Lezione 15 (8 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 13 (11 aprile
Subsections
Definizione 14.1
Un grafo
G è una coppia ordinata
G=(
V,
E) dove
V è un insieme detto
insieme dei
vertici del grafo ed
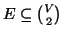
è detto
l'insieme dei
lati. Se
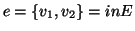
,
si dirà che il lato
e congiunge i due vertici
v1 e
v2.
Se G è un grafo, indicheremo con V(G) l'insieme dei suoi vertici e con
E(G) l'insieme dei suoi lati, ovvero
G=(V(G),E(G)).
Se G=(V,E) è un grafo e 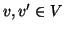 si dirà
che v e v' sono adiacenti o che v' è vicino a v se
si dirà
che v e v' sono adiacenti o che v' è vicino a v se
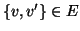 (cfr. esercizio 14.1).
(cfr. esercizio 14.1).
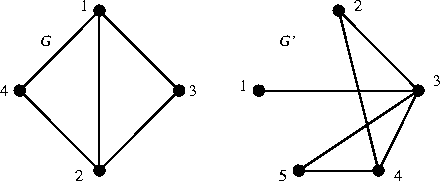
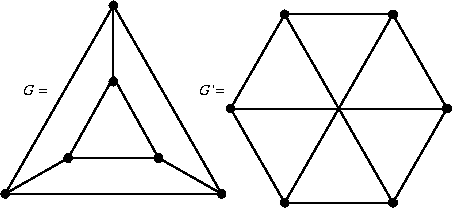
Spesso i grafi sono rappresentati graficamente mediante dei punti a
rappresentare i vertici e delle linee congiungenti due vertici a rappresentare i
lati. Ad esempio in figura 2 sono rappresentati i
grafi G e G'definiti da
Figure 2:
Esempi di grafi
 |
Esercizio 14.1
Sia (
V,
E) un grafo e si definisca la relazione
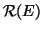
su
V ponendo
Si provi che:
- 1.
-
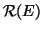 è simmetrica
(i.e.
è simmetrica
(i.e.
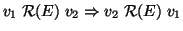 )
)
- 2.
-
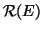 è antiriflessiva
(i.e.
è antiriflessiva
(i.e.
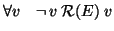 )
)
La relazione
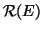
è a volte detta relazione di
adiacenza.
Soluzione
Esercizio 14.2
Sia
V un insieme, e sia
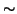
una relazione antiriflessiva su
V. Si
definisca
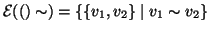
.
Si provi che
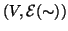
è un grafo.
Soluzione
Osservazione 14.2
Gli esercizi precedenti provano che dare un grafo i cui vertici sono l'insieme
V è equivalente a dare una relazione simmetrica e antiriflessiva su
V.
Diamo alcuni esempi di grafi notevoli, per i quali esiste anche una notazione
standard.
Per ogni
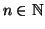 indicheremo con Pn il grafo tale che
indicheremo con Pn il grafo tale che
Pn è detto il cammino di lunghezza n (i.e. ha n lati).
Indicheremo con 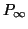 il grafo
il grafo
Pn è detto il cammino infinito.
Per ogni
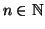 ,
,
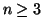 indicheremo con Cn il grafo tale che
indicheremo con Cn il grafo tale che
Cn è detto il ciclo di lunghezza n (i.e. ha n lati e nvertici).
Per ogni
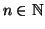 ,
indicheremo con Kn il grafo tale che
,
indicheremo con Kn il grafo tale che
Kn è detto il grafo completo su n vertici (i.e. ha tutti i lati
possibili che congiungono i suoi n vertici).
Per ogni
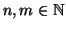 ,
indicheremo con Kn,m il grafo tale che
,
indicheremo con Kn,m il grafo tale che
Kn è detto il grafo completo bipartito su n ed m vertici (i.e.
ha tutti i lati possibili che congiungono i suoi primi n vertici con gli altri
m).
Isomorfismo di grafi
Definizione 14.3
Due grafi
G=(
V,
E) e
G'=(
V',
E') si dicono
isomorfi, e si denoterà
con
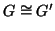
,
se e siste una bigezione
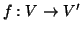
tale che
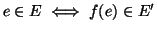
,
dove se
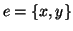
si è denotato
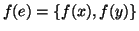
.
Una
tale applicazione
f sarà detta un
isomorfismo tra
G e
G'.
Esercizio 14.5
Si provi che i due grafi rappresentati in figura
3 sono tra
loro isomorfi.
Figure 3:
I grafi di esercizio 14.5
 |
Soluzione
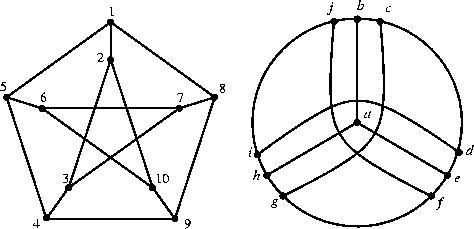
Esercizio 14.6
Dire se i due grafi in figura
4 sono isomorfi oppure no.
Figure 4:
I grafi dell'esercizio 14.6
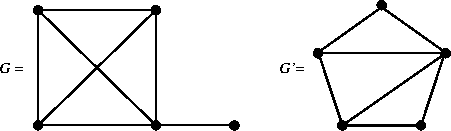 |
Soluzione
Esercizio 14.7
Provare che i due grafi in figura
5 non sono isomorfi.
Figure 5:
I grafi dell'esercizio 14.7
 |
Soluzione
Esercizio 14.8
Sia
G il grafo dato dai vertici e dagli spigoli di un cubo e sia
G' il
grafo tale che
V(
G') sia l'insieme delle parole di tre lettere nell'alfabeto
di due lettere
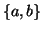
ed in cui due parole sono congiunte da un lato se e
solo se differiscono per una lettera soltanto. Si provi che
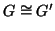
.
Soluzione



Next: Lezione 15 (8 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 13 (11 aprile
Domenico Luminati
2000-06-14
![]() si dirà
che v e v' sono adiacenti o che v' è vicino a v se
si dirà
che v e v' sono adiacenti o che v' è vicino a v se
![]() (cfr. esercizio 14.1).
(cfr. esercizio 14.1).
![]() indicheremo con Pn il grafo tale che
indicheremo con Pn il grafo tale che
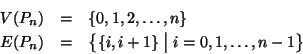
![]() il grafo
il grafo
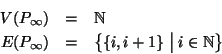
![]() ,
,
![]() indicheremo con Cn il grafo tale che
indicheremo con Cn il grafo tale che
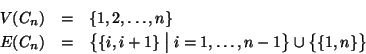
![]() ,
indicheremo con Kn il grafo tale che
,
indicheremo con Kn il grafo tale che
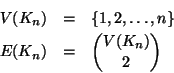
![]() ,
indicheremo con Kn,m il grafo tale che
,
indicheremo con Kn,m il grafo tale che