Soluzione dell'esercizio 1.10 Siano
![]() e
e
![]() due bigezioni, allora l'applicazione
due bigezioni, allora l'applicazione
![]() definita da
definita da
Per la seconda parte si osservi innanzitutto che
![]() e che
e che
![]() e che quindi per l'esercizio precedente,
e che quindi per l'esercizio precedente,
Soluzione dell'esercizio 1.11 Procediamo per induzione su n. Se n=1 non c'è nulla da
dimostrare. Supponiamo la tesi vera per n, usando l'associatività
dell'unione si ha
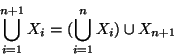
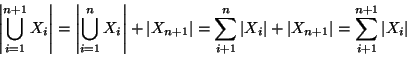
Soluzione dell'esercizio 2.1 Se una tale g esiste, f è surgettiva, dato che per ogni ![]() si ha che f(g(y))=y.
si ha che f(g(y))=y.
Viceversa, supponiamo che f sia surgettiva, allora
![]() per
ogni
per
ogni ![]() ,
per l'assioma di scelta, esiste una funzione di scelta,
,
per l'assioma di scelta, esiste una funzione di scelta,
![]() ,
tale che
,
tale che
![]() per ogni
per ogni ![]() ,
ma ciò
significa che f(g(y))=y per ogni
,
ma ciò
significa che f(g(y))=y per ogni ![]() ,
ossia che g è una inversa
destra di f.
,
ossia che g è una inversa
destra di f.
![]()
Soluzione dell'esercizio 2.2 Se una tale g esiste allora f deve necessariamente essere iniettiva, infatti
se
f(x1)=f(x2) allora
x1=g(f(x1))=g(f(x2))x2.
Viceversa, supponiamo che f sia iniettiva. Allora per ogni ![]() esiste
un unico
esiste
un unico ![]() tale che f(xy)=y. Preso un arbitrario
tale che f(xy)=y. Preso un arbitrario
![]() definiamo
definiamo ![]() ponendo
ponendo
Soluzione dell'esercizio 2.4 A partire dagli Xm costruiamo dei nuovi insiemi, ponendo
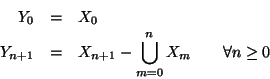
Soluzione dell'esercizio 2.5 Come nell'esercizio precedente, poniamo
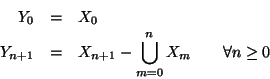
Soluzione dell'esercizio 3.3 La funzione
![]() definita da
definita da
![]() è una bigezione.
è una bigezione.
![]()
Soluzione dell'esercizio 3.4 Osserviamo che X-Y non può essere né finito né numerabile, altrimenti
![]() sarebbe numerabile. Ma allora X-Ycontiene un
sottinsieme, Y', numerabile. Dato che Y e Y' sono entrambi numerabili, la
loro unione è numerabile, sia quindi
sarebbe numerabile. Ma allora X-Ycontiene un
sottinsieme, Y', numerabile. Dato che Y e Y' sono entrambi numerabili, la
loro unione è numerabile, sia quindi
![]() una
bigezione e si definisca
una
bigezione e si definisca
![]() ponendo:
ponendo:
Soluzione dell'esercizio 3.5 Per ogni
![]() sia
sia
![]() .
Chiaramente
.
Chiaramente
![]() .
Proviamo che
.
Proviamo che
![]() per ogni
per ogni ![]() .
Procediamo per induzione su k. Se k=1 allora l'applicazione
.
Procediamo per induzione su k. Se k=1 allora l'applicazione
![]() è una bigezione
è una bigezione
![]() .
Supponiamo che Fk sia numerabile, allora per
ogni
.
Supponiamo che Fk sia numerabile, allora per
ogni ![]() sia
sia
![]() .
per ogni Al'insieme
Fk+1(A) è numerabile, in quanto in bigezione con
.
per ogni Al'insieme
Fk+1(A) è numerabile, in quanto in bigezione con
![]() ,
inoltre
,
inoltre
![]() è numerabile in quanto
unione di una famiglia numerabile di insiemi numerabili.
è numerabile in quanto
unione di una famiglia numerabile di insiemi numerabili.
![]()
Soluzione dell'esercizio 5.3 Si osservi che se X è un insieme con n elementi, allora
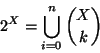
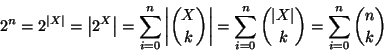
Soluzione dell'esercizio 6.1 Procediamo per induzione su k. Se k=1 non c'è nulla da
dimostrare. Supponiamo che la tesi sia vera per k e supponiamo che
![]() ,
ossia
,
ossia
![]() .
Per il corollario 6.3, si ha che
.
Per il corollario 6.3, si ha che
![]() oppure
oppure
![]() .
Se si verifica la seconda
eventualità abbiamo finito, altrimenti, per ipotesi di induzione esiste
.
Se si verifica la seconda
eventualità abbiamo finito, altrimenti, per ipotesi di induzione esiste
![]() tale che
tale che
![]() ,
e quindi si conclude.
,
e quindi si conclude.
![]()
Soluzione dell'esercizio 6.4 Chiaramente
![]() è un divisore comune a n e
m. Inoltre se c è un divisore comune non può avere fattori primi
diversi dai pi, quindi
è un divisore comune a n e
m. Inoltre se c è un divisore comune non può avere fattori primi
diversi dai pi, quindi
![]() .
Dal fatto che
.
Dal fatto che
![]() segue allora che
segue allora che
![]() e dal fatto che
e dal fatto che
![]() segue che
segue che
![]() per ogni i, e quindi
per ogni i, e quindi
![]() .
.
La formula per il m.c.m. segue allora dal fatto che
![]() ,
e
che per ogni coppia di numeri reali si ha che
,
e
che per ogni coppia di numeri reali si ha che
![]() .
.
![]()
Soluzione dell'esercizio 9.2 Osserviamo che
![]() se e solo se
se e solo se
![]() o
o
![]() ,
ma i
numeri più piccoli di pq che sono divisibili per p sono p,
,
ma i
numeri più piccoli di pq che sono divisibili per p sono p,
![]() ,
quelli che sono divisibili per q sono invece q,
,
quelli che sono divisibili per q sono invece q,
![]() e quindi i
numeri più piccoli di pq e non coprimi con pq sono p+q-1. Quindi
e quindi i
numeri più piccoli di pq e non coprimi con pq sono p+q-1. Quindi
![]() .
.
![]()
Soluzione dell'esercizio 9.3
![]() da cui
da cui
![]() .
Quindi
p e q sono determinati dal sistema di equazioni
.
Quindi
p e q sono determinati dal sistema di equazioni
Soluzione dell'esercizio 14.5 La colorazione dei lati data in figura 13
Soluzione dell'esercizio 14.8 Se identifichiamo la lettera a con il numero 0 e la b con l'1, si
ottiene una identificazione delle parole con le coordinate dei vertici del cubo
di
![]() dato da
dato da
![]() .
Inoltre due vertici di tale
cubo sono congiunti da uno spigolo se solo se differiscono esattamente per una
coordinata. L'identificazione data è quindi un isomorfismo di grafi tra G e
G'.
.
Inoltre due vertici di tale
cubo sono congiunti da uno spigolo se solo se differiscono esattamente per una
coordinata. L'identificazione data è quindi un isomorfismo di grafi tra G e
G'.
Soluzione dell'esercizio 19.7 Procediamo per induzione sul numero dei lati. Se
![]() il grafo ha un
solo vertice e quindi è lui stesso un albero.
il grafo ha un
solo vertice e quindi è lui stesso un albero.
Supponiamo che
![]() ,
allora s. Se per ogni
,
allora s. Se per ogni ![]() ,
G-e è
sconnesso, allora per la terza delle proprietà che caratterizzano
gli alberi, si ha che G è un albero. Se invece esiste un
e tale che G-e è connesso, allora, avendo un lato in meno di G, per
ipotesi di induzione G-e ha un per sottografo un albero che contiene tutti i
suoi vertici (e quindi tutti i vertici di G). Chiaramente questo sottografo
è sottografo anche di G.
,
G-e è
sconnesso, allora per la terza delle proprietà che caratterizzano
gli alberi, si ha che G è un albero. Se invece esiste un
e tale che G-e è connesso, allora, avendo un lato in meno di G, per
ipotesi di induzione G-e ha un per sottografo un albero che contiene tutti i
suoi vertici (e quindi tutti i vertici di G). Chiaramente questo sottografo
è sottografo anche di G.
![]()
Soluzione dell'esercizio 19.8 Sia T un albero generatore di G. Chiaramente
![]() e
dato che T è un sottografo di G allora
e
dato che T è un sottografo di G allora
![]() e
quindi, usando la formula che lega il numero di lati con il numero dei
vertici di un grafo, si ha
e
quindi, usando la formula che lega il numero di lati con il numero dei
vertici di un grafo, si ha
Soluzione dell'esercizio 20.2 Si definisce passeggiata diretta una successione finita di vertici
![]() tali che
tali che
![]() per ogni i. Una passeggiata
diretta si dirà un cammino diretto se e solo se i vertici v1 sono a due a
due distinti, una passeggiata diretta si dirà un ciclo diretto se e solo se i
vertici sono a due a due distinti a parte il primo e l'ultimo che coincidono.
per ogni i. Una passeggiata
diretta si dirà un cammino diretto se e solo se i vertici v1 sono a due a
due distinti, una passeggiata diretta si dirà un ciclo diretto se e solo se i
vertici sono a due a due distinti a parte il primo e l'ultimo che coincidono.
Proviamo che se due vertici sono congiungibili da una passeggiata diretta,
allora sono congiungibili da un cammino diretto. Siano v, ![]() e sia
e sia
![]() una passeggiata diretta di lunghezza minima che
congiunge v e w e proviamo che P è un cammino diretto. Infatti se per
assurdo vi=vj con i<j allora
una passeggiata diretta di lunghezza minima che
congiunge v e w e proviamo che P è un cammino diretto. Infatti se per
assurdo vi=vj con i<j allora
![]() sarebbe
ancora una passeggiata diretta tra v e w, ma ciò è in contraddizione con
il fatto che P sia di lunghezza minima.
sarebbe
ancora una passeggiata diretta tra v e w, ma ciò è in contraddizione con
il fatto che P sia di lunghezza minima.
La riflessività è ovvia (basta prendere cammini di lunghezza 0, e la transitività, come nel caso dei grafi, si prova congiungendo due passeggiate.
L'essere congiungibili da un cammino diretto non è una relazione
d'equivalenza. Basta considerare il seguente esempio: ![]() e
e
![]() .
0 è congiungibile a 1 ma non il viceversa.
.
0 è congiungibile a 1 ma non il viceversa.
![]()
Soluzione dell'esercizio 20.3
![]() se e solo se esiste
se e solo se esiste ![]() tale che
tale che
![]() e
e
![]() e quest'ultima è vera se e solo se esiste
e quest'ultima è vera se e solo se esiste ![]() tale
che
tale
che
![]() e
e
![]() .
In definitiva
.
In definitiva