


Next: Lezione 10 (28 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 8 (21 marzo
Subsections
Definizione 9.1
Dati due interi
n,
m si dice che
n è un
divisore di
m (o che
m è un
multiplo di
n) se esiste un
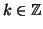
tale
che
m=
nk. Si indica con
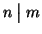
(si legge
n divide
m).
Esempio 9.2
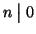
per ogni
n mentre se
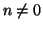
allora
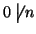
,
si ha
inoltre che
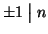
e
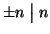
per ogni
n.
Dimostrazione.
1. Se m=kn e q=hm allora
q=hkm=(hk)m ossia
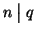 .
.
2. Se n=mk e m=nh allora m=hkm e quindi
m(1-hk)=0 e quindi o m=0 e quindi anche n=0, oppure 1-hk=0 ma
allora o h=k=1 e quindi n=m oppure n=m=-1 e quindi n=-m.

Definizione 9.4
Il numero
n si dice
primo se i suoi unici divisori sono
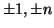
.
Definizione 9.5
Dati due interi
n,
m non entrambi nulli, si dice che
d è
un massimo comun divisoretra
n e
m se:
- 1.
-
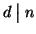 e
e
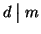 ;
;
- 2.
- Se
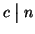 e
e
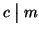 allora
allora
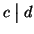 .
.
Proposizione 9.6
Se
d e
d' sono due massimi comun divisori tra
n e
m allora
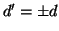
.
Dimostrazione.
d è un divisore comune di n e m, quindi poiché d'è un massimo comun divisore si ha che
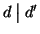 .
Scambiando i
ruoli di d e d' si ha allora che anche
.
Scambiando i
ruoli di d e d' si ha allora che anche
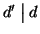 e quindi per
9.3 si ha che
e quindi per
9.3 si ha che 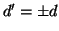 .
.

Definizione 9.7
Diremo che d è il massimo comun divisore di n e m se
è un massimo comun divisore positivo. La proposizione precedente
garantisce che se esiste il massimo comun divisore è unico. Esso
verrà indicato con (n,m).
Teorema 9.8
Dati due numeri
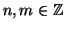
non entrambi nulli esiste il massimo
comun divisore di
n ed
m.
Dimostrazione.
Si consideri l'insieme
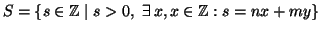 .
.
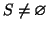 dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
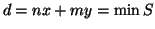 ,
dimostriamo che dè il massimo comun divisore. Se
,
dimostriamo che dè il massimo comun divisore. Se
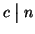 e
e
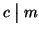 allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
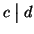 .
Dimostriamo ora che
.
Dimostriamo ora che
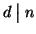 .
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con
.
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con 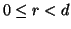 ,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e
,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e 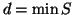 .
Quindi r=0 ossia
.
Quindi r=0 ossia
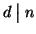 .
In modo analogo si prova che
.
In modo analogo si prova che
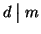 .
.

Osservazione 9.9
Dalla dimostrazione precedente segue che dati
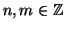
esistono
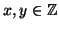
tali che
(
n,
m)=
nx+
my e che gli interi della forma
nx+
my con
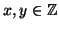
sono tutti e soli i multipli di (
n,
m).
Definizione 9.10
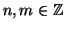
non entrambi nulli si dicono
coprimi se (
n,
m)=1.
Osservazione 9.11
(
n,
m)=1 se e solo se esistono
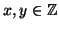
tali che
nx+
my=1. Ad
esempio (
n,
n+1)=1 per ogni
n. Infatti
1=(
n+1)1+
n(-1).
Proposizione 9.12
Sia
d=(
n,
m), allora
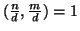
.
Dimostrazione.
d=nx+my e quindi
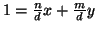 .
.

Proposizione 9.13 (algoritmo di Euclide)
Siano
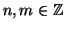
,
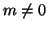
.
Sia
n=
mq+
r la divisione euclidea di
n per
m allora
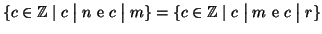
,
in
particolare quindi
(
n,
m)=(
m,
r).
Dimostrazione.
Se
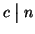 e
e
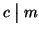 allora n=ch e m=ck e quindi
r=n-mq=ch-ckq=c(h-kq) ossia
allora n=ch e m=ck e quindi
r=n-mq=ch-ckq=c(h-kq) ossia
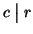 e
e
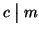 .
Viveversa
se
.
Viveversa
se
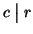 e
e
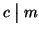 allora m=ch e r=ck e quindi
n=mq+r=chq+ck=c(hq+r) ossia
allora m=ch e r=ck e quindi
n=mq+r=chq+ck=c(hq+r) ossia
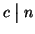 e
e
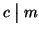 .
.

La proposizione precedente assieme all'osservazione che (n,0)=n per
ogni 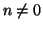 permette di costruire un algoritmo (algoritmo di
Euclide) per il calcolo del M.C.D.
permette di costruire un algoritmo (algoritmo di
Euclide) per il calcolo del M.C.D.



Next: Lezione 10 (28 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 8 (21 marzo
Domenico Luminati
2001-06-18
![]() .
.
![]()
![]() .
Scambiando i
ruoli di d e d' si ha allora che anche
.
Scambiando i
ruoli di d e d' si ha allora che anche
![]() e quindi per
9.3 si ha che
e quindi per
9.3 si ha che ![]() .
.
![]()
![]() .
.
![]() dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
![]() ,
dimostriamo che dè il massimo comun divisore. Se
,
dimostriamo che dè il massimo comun divisore. Se
![]() e
e
![]() allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
![]() .
Dimostriamo ora che
.
Dimostriamo ora che
![]() .
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con
.
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con ![]() ,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e
,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e ![]() .
Quindi r=0 ossia
.
Quindi r=0 ossia
![]() .
In modo analogo si prova che
.
In modo analogo si prova che
![]() .
.
![]()
![]() .
.
![]()
![]() e
e
![]() allora n=ch e m=ck e quindi
r=n-mq=ch-ckq=c(h-kq) ossia
allora n=ch e m=ck e quindi
r=n-mq=ch-ckq=c(h-kq) ossia
![]() e
e
![]() .
Viveversa
se
.
Viveversa
se
![]() e
e
![]() allora m=ch e r=ck e quindi
n=mq+r=chq+ck=c(hq+r) ossia
allora m=ch e r=ck e quindi
n=mq+r=chq+ck=c(hq+r) ossia
![]() e
e
![]() .
.
![]()
![]() permette di costruire un algoritmo (algoritmo di
Euclide) per il calcolo del M.C.D.
permette di costruire un algoritmo (algoritmo di
Euclide) per il calcolo del M.C.D.
