- se
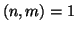 e
e
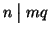 allora
allora
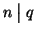 .
.
- se
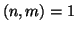 e
e
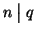 e
e
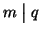 allora
allora
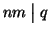 .
.
Dimostrazione.
1. Se ![]() allora esistono
allora esistono
![]() tali che
tali che ![]() e quindi
e quindi ![]() . Ma allora se
. Ma allora se
![]() esiste
esiste ![]() tale che
tale che
![]() e quindi
e quindi
![]() .
.
2.
![]() quindi
quindi ![]() , dato che
, dato che
![]() e
e ![]() allora per la 1 si ha che
allora per la 1 si ha che
![]() ossia
ossia ![]() e quindi
e quindi
![]() , ovvero
, ovvero
![]() .
.
![]()
Dimostrazione.
Supponiamo che
![]() , dato che
, dato che ![]() è primo, se
è primo, se
![]() allora
allora ![]() , per lo proposizione precedente si
ha allora che
, per lo proposizione precedente si
ha allora che
![]() .
.
Viceversa supponiamo che per ogni
![]() si ha che
si ha che
![]() oppure
oppure
![]() , allora se
, allora se ![]() allora
allora
![]() e quindi
e quindi
![]() , e quindi per 9.3 si
ha che
, e quindi per 9.3 si
ha che ![]() e
e ![]() oppure
oppure
![]() e quindi
e quindi ![]() e
e
![]() .
.
![]()
Dimostrazione.
Sia
![]() dove si è posto
dove si è posto ![]() e
e
![]() . Chiaramente allora
. Chiaramente allora ![]() e quindi
e quindi
![]() e
e
![]() .
.
Se
![]() e
e
![]() allora
allora
![]() e quindi
posto
e quindi
posto ![]() si ha che
si ha che
![]() e
e
![]() . Dato
che
. Dato
che ![]() , per 10.1 si ha che
, per 10.1 si ha che
![]() e
quindi che
e
quindi che
![]() .
.
![]()
In altre parole, ogni intero maqggiore di ![]() si scrive in modo
unico, a meno dell'ordine, come prodotto di numeri primi positivi.
si scrive in modo
unico, a meno dell'ordine, come prodotto di numeri primi positivi.
Dimostrazione.
Procediamo per induzione su ![]() . Se
. Se ![]() non c'è nulla da
dimostrare in quanto
non c'è nulla da
dimostrare in quanto ![]() è primo. Supponiamo
è primo. Supponiamo ![]() e che la tesi sia
vera per ogni
e che la tesi sia
vera per ogni ![]() . Se
. Se ![]() è primo non c'è nulla da dimostrare,
se
è primo non c'è nulla da dimostrare,
se ![]() non è primo allora esistono due numeri
non è primo allora esistono due numeri ![]() con
con
![]() tali che
tali che ![]() . Per ipotesi di induzione esistono
dei primi positivi
. Per ipotesi di induzione esistono
dei primi positivi ![]() e
e ![]() tali che
tali che
![]() e
e
![]() , ma allora
, ma allora
![]() è prodotto di primi positivi.
è prodotto di primi positivi.
Unicità. Sia
![]() con
con ![]() e
e ![]() primi
positivi e
primi
positivi e ![]() . Procediamo per induzione su
. Procediamo per induzione su ![]() . Se
. Se ![]() allora
allora
![]() , quindi
, quindi
![]() per ogni
per ogni ![]() , e dato che
, e dato che
![]() è primo ogni
è primo ogni ![]() oppure
oppure ![]() . Poiché per ipotesi
ogni
. Poiché per ipotesi
ogni ![]() allora
allora ![]() per ogni
per ogni ![]() . Se ora fosse
. Se ora fosse ![]() si
avrebbe
si
avrebbe
![]() e questo è assurdo, e
quindi
e questo è assurdo, e
quindi ![]() e
e ![]() .
.
Sia ![]() , allora
, allora
![]() , quindi per l'esercizio
10.1 esiste un
, quindi per l'esercizio
10.1 esiste un ![]() tale che
tale che
![]() . Dato che sia
. Dato che sia ![]() che
che ![]() sono primi positivi, allora
sono primi positivi, allora ![]() . Ma allora
. Ma allora
![]() , per ipotesi di induzione
possiamo allora dire che le due fattorizzazioni hanno lo stesso numero
di elementi, ossia
, per ipotesi di induzione
possiamo allora dire che le due fattorizzazioni hanno lo stesso numero
di elementi, ossia ![]() , e che esiste una bigezione
, e che esiste una bigezione
![]() tale che
tale che
![]() per ogni
per ogni ![]() . Definendo allora
. Definendo allora
![]()
Dimostrazione.
Per assurdo supponiamo che
![]() siano tutti
iprimi. Si consideri
siano tutti
iprimi. Si consideri
![]() . Chiaramente
. Chiaramente ![]() e non
è divisibile per nessun
e non
è divisibile per nessun ![]() e quindi
e quindi ![]() sarebbe un numero
maggiore di
sarebbe un numero
maggiore di ![]() che non è divisibile per nessun primo e ciò
contraddice il teorema fondamentale dell'aritmetica.
che non è divisibile per nessun primo e ciò
contraddice il teorema fondamentale dell'aritmetica.
![]()
Siano
![]() ,
,
![]() con
con ![]() numeri primi, allora
numeri primi, allora
![]() e
e
![]() .
.
Soluzione