Soluzione dell'esercizio 3.2 Proviamo soltanto l'associatività della somma. Dobbiamo provare che per ogni
![]() si ha che
si ha che
![]() .
Procediamo per induzione su
.
Procediamo per induzione su ![]() . Se
. Se ![]() dalla definizione si ha
dalla definizione si ha ![]() e anche
e anche
![]() . Supponiamo la tesi vera per
. Supponiamo la tesi vera per ![]() e proviamola
per
e proviamola
per
![]() .
.
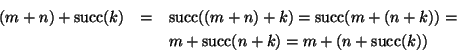
Soluzione dell'esercizio 4.2 Siano ![]() e
e ![]() due bigezioni, allora l'applicazione
due bigezioni, allora l'applicazione
![]() definita da
definita da
Per la seconda parte si osservi innanzitutto che
![]() e che
e che
![]() e che quindi per l'esercizio precedente,
e che quindi per l'esercizio precedente,
Soluzione dell'esercizio 4.3 Procediamo per induzione su ![]() . Se
. Se ![]() non c'è nulla da
dimostrare. Supponiamo la tesi vera per
non c'è nulla da
dimostrare. Supponiamo la tesi vera per ![]() , usando l'associatività
dell'unione si ha
, usando l'associatività
dell'unione si ha
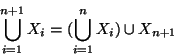
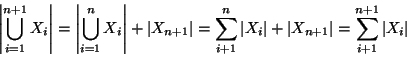
Soluzione dell'esercizio 5.1 Se una tale ![]() esiste,
esiste, ![]() è surgettiva, dato che per ogni
è surgettiva, dato che per ogni ![]() si ha che
si ha che ![]() .
.
Viceversa, supponiamo che ![]() sia surgettiva, allora
sia surgettiva, allora
![]() per
ogni
per
ogni ![]() , per l'assioma di scelta, esiste una funzione di scelta,
, per l'assioma di scelta, esiste una funzione di scelta,
![]() , tale che
, tale che
![]() per ogni
per ogni ![]() , ma ciò
significa che
, ma ciò
significa che ![]() per ogni
per ogni ![]() , ossia che
, ossia che ![]() è una inversa
destra di
è una inversa
destra di ![]() .
.
![]()
Soluzione dell'esercizio 5.2 Se una tale ![]() esiste allora
esiste allora ![]() deve necessariamente essere iniettiva, infatti
se
deve necessariamente essere iniettiva, infatti
se ![]() allora
allora
![]() .
.
Viceversa, supponiamo che ![]() sia iniettiva. Allora per ogni
sia iniettiva. Allora per ogni ![]() esiste
un unico
esiste
un unico ![]() tale che
tale che ![]() . Preso un arbitrario
. Preso un arbitrario
![]() definiamo
definiamo ![]() ponendo
ponendo
Soluzione dell'esercizio 6.2 A partire dagli ![]() costruiamo dei nuovi insiemi, ponendo
costruiamo dei nuovi insiemi, ponendo
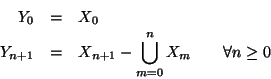
Soluzione dell'esercizio 6.3 Come nell'esercizio precedente, poniamo
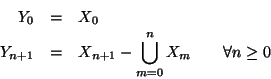
Soluzione dell'esercizio 6.7 La funzione
![]() definita da
definita da
![]() è una bigezione.
è una bigezione.
![]()
Soluzione dell'esercizio 6.8 Osserviamo che ![]() non può essere né finito né numerabile, altrimenti
non può essere né finito né numerabile, altrimenti
![]() sarebbe numerabile. Ma allora
sarebbe numerabile. Ma allora ![]() contiene un
sottinsieme,
contiene un
sottinsieme, ![]() , numerabile. Dato che
, numerabile. Dato che ![]() e
e ![]() sono entrambi numerabili, la
loro unione è numerabile, sia quindi
sono entrambi numerabili, la
loro unione è numerabile, sia quindi
![]() una
bigezione e si definisca
una
bigezione e si definisca ![]() ponendo:
ponendo:
Soluzione dell'esercizio 6.9 Per ogni
![]() sia
sia
![]() . Chiaramente
. Chiaramente
![]() . Proviamo che
. Proviamo che
![]() per ogni
per ogni ![]() . Procediamo per induzione su
. Procediamo per induzione su ![]() . Se
. Se ![]() allora l'applicazione
allora l'applicazione ![]() è una bigezione
è una bigezione
![]() . Supponiamo che
. Supponiamo che ![]() sia numerabile, allora per
ogni
sia numerabile, allora per
ogni ![]() sia
sia
![]() . per ogni
. per ogni ![]() l'insieme
l'insieme ![]() è numerabile, in quanto in bigezione con
è numerabile, in quanto in bigezione con ![]() ,
inoltre
,
inoltre
![]() è numerabile in quanto
unione di una famiglia numerabile di insiemi numerabili.
è numerabile in quanto
unione di una famiglia numerabile di insiemi numerabili.
![]()
DIVE (n,m) {
N=n
M=m
Q=0
R=N
WHILE N > M-1 DO
N = N-M
R = N
Q = Q+1
END WHILE
}
Soluzione dell'esercizio 8.1 Dalla definizione del coefficiente binomiale si ha
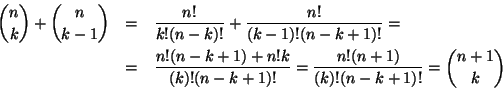
Soluzione dell'esercizio 8.2 Si osservi che se ![]() è un insieme con
è un insieme con ![]() elementi, allora
elementi, allora
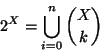
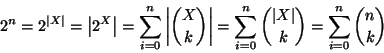
Soluzione dell'esercizio 10.1 Procediamo per induzione su ![]() . Se
. Se ![]() non c'è nulla da
dimostrare. Supponiamo che la tesi sia vera per
non c'è nulla da
dimostrare. Supponiamo che la tesi sia vera per ![]() e supponiamo che
e supponiamo che
![]() , ossia
, ossia
![]() . Per il corollario 10.2, si ha che
. Per il corollario 10.2, si ha che
![]() oppure
oppure
![]() . Se si verifica la seconda
eventualità abbiamo finito, altrimenti, per ipotesi di induzione esiste
. Se si verifica la seconda
eventualità abbiamo finito, altrimenti, per ipotesi di induzione esiste
![]() tale che
tale che
![]() , e quindi si conclude.
, e quindi si conclude.
![]()
Soluzione dell'esercizio 10.4 Chiaramente
![]() è un divisore comune a
è un divisore comune a ![]() e
e
![]() . Inoltre se
. Inoltre se ![]() è un divisore comune non può avere fattori primi
diversi dai
è un divisore comune non può avere fattori primi
diversi dai ![]() , quindi
, quindi
![]() . Dal fatto che
. Dal fatto che
![]() segue allora che
segue allora che ![]() e dal fatto che
e dal fatto che
![]() segue che
segue che ![]() per ogni
per ogni ![]() , e quindi
, e quindi
![]() .
.
La formula per il m.c.m. segue allora dal fatto che
![]() , e
che per ogni coppia di numeri reali si ha che
, e
che per ogni coppia di numeri reali si ha che
![]() .
.
![]()
Soluzione dell'esercizio 11.1 Per quanto visto nell'osservazione 11.8, possiamo definire
l'applicazione ![]() data da
data da
![]() .
.
Data invece una partizione ![]() definiamo la relazione
definiamo la relazione
![]() ponendo
ponendo
![]() è riflessiva. Se
è riflessiva. Se ![]() allora, dato che
allora, dato che ![]() ricopre
ricopre ![]() (proprietà (2) di 11.8), esiste
(proprietà (2) di 11.8), esiste ![]() tale che
tale che ![]() e quindi
e quindi
![]() .
.
![]() è simmetrica. Ovvio.
è simmetrica. Ovvio.
![]() è transitiva. Siano
è transitiva. Siano
![]() e
e
![]() , allora esistono
, allora esistono
![]() tali che
tali che ![]() e
e ![]() . Ma, allora
. Ma, allora
![]() ossia
ossia
![]() e quindi coincidono (proprietà (3) di 11.8) ossia
e quindi coincidono (proprietà (3) di 11.8) ossia ![]() e
quindi
e
quindi ![]() ovvero
ovvero
![]() .
.
Definiamo allora ![]() ponendo
ponendo
![]() , e
proviamo che
, e
proviamo che
![]() e
e
![]() . Ciò concluderà la
dimostrazione.
. Ciò concluderà la
dimostrazione.
Sia ![]() , allora, per la (2) della proposizione
11.7, si ha che
, allora, per la (2) della proposizione
11.7, si ha che
![]() se e solo se
se e solo se
![]() ossia se e solo se esiste
ossia se e solo se esiste
![]() tale che
tale che ![]() ossia se e solo se esiste
ossia se e solo se esiste
![]() tale che
tale che ![]() ossia se e solo se
ossia se e solo se
![]() e
quindi
e
quindi
![]() .
.
Sia invece ![]() , allora, dato
, allora, dato ![]() sia
sia ![]() , è chiaro che
, è chiaro che
![]() , ciò unito al fatto che
, ciò unito al fatto che ![]() ricopre
ricopre ![]() (proprietà (2) di 11.8) permette di concludere che
(proprietà (2) di 11.8) permette di concludere che
![]() ovvero che
ovvero che
![]() .
.
![]()
Soluzione dell'esercizio 11.2 Proviamone l'ultima a titolo di esempio, le a ltre si dimostrano in modo
completamente analogo.
Soluzione dell'esercizio 12.2 Osserviamo che per ogni
![]() si ha che
si ha che
![]() . Questo perché
. Questo perché
![]() e quindi
e quindi
![]() . Ma allora
. Ma allora
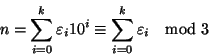
Del tutto analoga è la dimostrazione della seconda. Per quanto riguarda la
terza si adatti la dimostrazione della prima osservando che
![]() e quindi
e quindi
Soluzione dell'esercizio 13.1 Sia ![]() una soluzione di
una soluzione di
![]() , allora
, allora
![]() ossia
ossia
![]() . Ma allora
. Ma allora
![]() da cui segue che
da cui segue che
![]() , ossia
, ossia ![]() è una soluzione della seconda congruenza.
è una soluzione della seconda congruenza.
Viceversa se ![]() risolve
risolve
![]() allora esiste
allora esiste ![]() tale che
tale che
![]() e quindi
e quindi
![]() , ossia
, ossia ![]() risolve la
prima congruenza.
risolve la
prima congruenza.
![]()
Soluzione dell'esercizio 13.2 Se
![]() allora
allora
![]() , ma dato che
, ma dato che
![]() allora
anche
allora
anche
![]() , ovvero
, ovvero
![]() .
.
Proviamo innanzitutto che
![]() per ogni
per ogni
![]() . Infatti se
. Infatti se
![]() allora
allora
![]() e quindi
e quindi
![]() , da cui segue che
, da cui segue che
![]() ossia che
ossia che
![]() . Da questo fatto ne consegue allora che
. Da questo fatto ne consegue allora che
![]() . Dimostriamo l'inclusione
opposta. Sia
. Dimostriamo l'inclusione
opposta. Sia
![]() , e sia
, e sia ![]() il resto della divisione euclidea
di
il resto della divisione euclidea
di ![]() per
per ![]() , ossia
, ossia ![]() con
con ![]() . Allora
. Allora
![]() e
quindi
e
quindi
![]() , ovvero esiste
, ovvero esiste ![]() tale che
tale che ![]() e
e
![]() .
Inoltre
.
Inoltre ![]() e quindi
e quindi
![]() , ossia
, ossia
![]() .
.
Per concludere osserviamo che affinché si abbia
![]() deve aversi
deve aversi
![]() , ovvero
, ovvero
![]() . Supposto per assurdo che
. Supposto per assurdo che ![]() si ha allora che
si ha allora che ![]() e
quindi
e
quindi
![]() , ma allora
, ma allora ![]() non potrebbe essere un multiplo
di
non potrebbe essere un multiplo
di ![]() .
.
![]()
Soluzione dell'esercizio 13.3 Osserviamo che
![]() risolve l'equazione
risolve l'equazione
![]() se e solo se
se e solo se
![]() .
Per l'esercizio 13.1 se
.
Per l'esercizio 13.1 se ![]() è una soluzione intera allora tutte le
soluzioni intere sono
è una soluzione intera allora tutte le
soluzioni intere sono
![]() . Ma allora per l'esercizio
precedente
. Ma allora per l'esercizio
precedente
![]() e le classi
e le classi
![]() con
con
![]() sono tutte diverse. Queste sono tutte e sole le soluzioni in
sono tutte diverse. Queste sono tutte e sole le soluzioni in
![]() dell'equazione lineare
dell'equazione lineare
![]() .
.
![]()
Soluzione dell'esercizio 13.4 Sia
![]() allora o
allora o
![]() oppure
oppure ![]() , ma nel primo caso
, ma nel primo caso
![]() nel secondo caso
nel secondo caso
![]() è invertibile mod
è invertibile mod ![]() e
quindi
e
quindi
![]() ovvero
ovvero
![]() . Ne consegue che in ogni caso il prodotto di
. Ne consegue che in ogni caso il prodotto di
![]() e di
e di
![]() è
è
![]() ovvero
ovvero
![\begin{eqnarray*}
\left[0\right]_p
&=&\left[x\right]_p(\left[x\right]_p^{p-1}-...
...1}-1\right]_p=\left[x(x^{p-1}-1)\right]_p=\left[x^{p}-x\right]_p
\end{eqnarray*}](img1885.gif)
Soluzione dell'esercizio 13.5 Osserviamo che ![]() se e solo se
se e solo se
![]() o
o
![]() , ma i
numeri più piccoli di
, ma i
numeri più piccoli di ![]() che sono divisibili per
che sono divisibili per ![]() sono
sono ![]() ,
, ![]() ,
quelli che sono divisibili per
,
quelli che sono divisibili per ![]() sono invece
sono invece ![]() ,
, ![]() e quindi i
numeri più piccoli di
e quindi i
numeri più piccoli di ![]() e non coprimi con
e non coprimi con ![]() sono
sono ![]() . Quindi
. Quindi
![]() .
.
![]()
Soluzione dell'esercizio 13.6
![]() da cui
da cui
![]() . Quindi
. Quindi
![]() e
e ![]() sono determinati dal sistema di equazioni
sono determinati dal sistema di equazioni
Soluzione dell'esercizio 14.1 La relazione
![]() è simmetrica. Infatti se
è simmetrica. Infatti se
![]() . Ma
. Ma
![]() , quindi anche
, quindi anche
![]() e quindi
e quindi
![]() .
.
La relazione
![]() è antiriflessiva. Infatti per ogni
è antiriflessiva. Infatti per ogni ![]()
![]() e per tanto
e per tanto
![]() .
.
Se ![]() è antiriflessiva, allora
è antiriflessiva, allora
![]() ,
infatti se
,
infatti se
![]() allora, per definizione di
allora, per definizione di
![]() ,
, ![]() con
con ![]() , e dato che
, e dato che
![]() è antiriflessiva,
è antiriflessiva, ![]() e quindi
e quindi
![]() ovvero
ovvero
![]() ovvero
ovvero
![]() .
.
![]()
Soluzione dell'esercizio 14.2 Per quanto visto nell'osservazione 14.2, la relazione
![]() è
sempre simmetrica, quindi non potrà essere uguale a
è
sempre simmetrica, quindi non potrà essere uguale a ![]() che non lo è.
che non lo è.
Un esempio. ![]() e
e
![]() . Evidentemente
. Evidentemente ![]() ma
ma ![]() .
.
![]()
Soluzione dell'esercizio 14.4 Il sottografo indotto ![]() è isomorfo a
è isomorfo a ![]() . Sia
. Sia
![]() una funzione bigettiva.
una funzione bigettiva. ![]() è evidentemente un isomorfismo dato che tutte
le coppie di elemnti di
è evidentemente un isomorfismo dato che tutte
le coppie di elemnti di ![]() sono lati di
sono lati di ![]() e tutte le coppie
di eleenti
e tutte le coppie
di eleenti ![]() al variare di
al variare di
![]() sono lati di
sono lati di ![]() e
quindi di
e
quindi di ![]() .
.
Volendo essere più formali, dato che ![]() è completo, per ogni
è completo, per ogni
![]() il lato
il lato
![]() e
quindi
e
quindi
![]() . D'altra parte se
. D'altra parte se
![]() , allora esistono
, allora esistono ![]() tali che
tali che ![]() e
e ![]() e
dato che
e
dato che ![]() è il grafo completo,
è il grafo completo,
![]() .
.
![]()
Soluzione dell'esercizio 14.9 La colorazione dei lati data in figura 14
Soluzione dell'esercizio 14.10
Soluzione dell'esercizio 14.11
Soluzione dell'esercizio 14.12 Se identifichiamo la lettera ![]() con il numero
con il numero ![]() e la
e la ![]() con l'
con l'![]() , si
ottiene una identificazione delle parole con le coordinate dei vertici del cubo
di
, si
ottiene una identificazione delle parole con le coordinate dei vertici del cubo
di ![]() dato da
dato da
![]() . Inoltre due vertici di tale
cubo sono congiunti da uno spigolo se solo se differiscono esattamente per una
coordinata. L'identificazione data è quindi un isomorfismo di grafi tra
. Inoltre due vertici di tale
cubo sono congiunti da uno spigolo se solo se differiscono esattamente per una
coordinata. L'identificazione data è quindi un isomorfismo di grafi tra ![]() e
e
![]() .
.
Soluzione dell'esercizio 16.1 Chiaramente
![]() . Proviamo l'inclusione
opposta. Se
. Proviamo l'inclusione
opposta. Se ![]() allora
allora ![]() ed i vertici
ed i vertici ![]() sono
evidentemente congiungibili. Allora sono vertici di una medesima componente
connessa, ovvero esiste
sono
evidentemente congiungibili. Allora sono vertici di una medesima componente
connessa, ovvero esiste ![]() tale che
tale che ![]() . Per definizione di
componente connessa e di sottografo indotto
. Per definizione di
componente connessa e di sottografo indotto
![]() . Quindi, per
l'arbitrarietà di
. Quindi, per
l'arbitrarietà di ![]() se ne deduce che
se ne deduce che
![]() .
.
![]()
Soluzione dell'esercizio 16.2 Segue immediatamente dall'esercizio precedente e dall'osservare che gli insiemi
dei lati di due componenti diverse sono necessariamente disgiunti.
![]()
Soluzione dell'esercizio 16.3 Siano
![]() , dato che
, dato che ![]() è connesso esiste una passeggiata in
è connesso esiste una passeggiata in
![]() che li congiunge, sia questa
che li congiunge, sia questa
![]() . Ossia
. Ossia
![]() per ogni
per ogni ![]() . Ma dato che
. Ma dato che ![]() è un sottografo di
è un sottografo di
![]() , allora
, allora
![]() e quindi
e quindi
![]() per ogni
per ogni
![]() , ossia
, ossia ![]() è una passeggiata in
è una passeggiata in ![]() , quindi
, quindi ![]() sono congiungibili in
sono congiungibili in
![]() .
.
![]()
Soluzione dell'esercizio 19.1 Sia ![]() e siano
e siano
![]() , si hanno due casi:
, si hanno due casi:
Nel secondo caso, supponiamo che ![]() allora per il passo precedente sappiamo
che
allora per il passo precedente sappiamo
che ![]() è congiungibile con
è congiungibile con ![]() in
in ![]() , d'altra parte
, d'altra parte ![]() è congiungbile
con
è congiungbile
con ![]() e quindi
e quindi ![]() è congiungibile con
è congiungibile con ![]() .
.
![]()
Soluzione dell'esercizio 19.2 Sia
![]() , allora
, allora
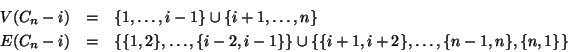
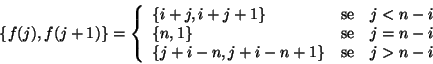
Soluzione dell'esercizio 19.3 Sia ![]() hamiltoniano, e sia
hamiltoniano, e sia ![]() un sottografo di
un sottografo di ![]() isomorfo a
isomorfo a ![]() che
contiene tutti i vertici di
che
contiene tutti i vertici di ![]() . Allora
. Allora ![]() è un sottografo di
è un sottografo di ![]() che
contiene tutti i vertici di
che
contiene tutti i vertici di ![]() . Ma
. Ma ![]() è isomorfo a un cammino
(esercizio precedente) che è connesso. Si
conclude allora invocando l'esercizio 16.3.
è isomorfo a un cammino
(esercizio precedente) che è connesso. Si
conclude allora invocando l'esercizio 16.3.
![]()
Soluzione dell'esercizio 19.5 Usando l'esercizio precedente, possiamo supporre che ![]() . Ma allora si
verifica immediatamente che la funzione
. Ma allora si
verifica immediatamente che la funzione
![]() definita da
definita da
Soluzione dell'esercizio 19.6 Possiamo supporre che ![]() . Ma allora si
verifica immediatamente che la funzione
. Ma allora si
verifica immediatamente che la funzione
![]() definita da
definita da
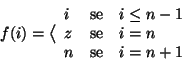
Soluzione dell'esercizio 19.10
Soluzione dell'esercizio 19.11
Soluzione dell'esercizio 19.12
Soluzione dell'esercizio 19.13
Soluzione dell'esercizio 20.3 Un cammino in ![]() che congiunge due vertici diversi da
che congiunge due vertici diversi da ![]() non può passare
per
non può passare
per ![]() , in quanto i vertici di un cammino, eccetto al più il primo e
l'ultimo, hanno grado almeno
, in quanto i vertici di un cammino, eccetto al più il primo e
l'ultimo, hanno grado almeno ![]() .
.
![]()
Soluzione dell'esercizio 20.4 Per l'esercizio precedente ![]() è connesso. D'altra parte se
è connesso. D'altra parte se ![]() avesse un ciclo,
questo sarebbe un ciclo anche in
avesse un ciclo,
questo sarebbe un ciclo anche in ![]() .
.
![]()
Soluzione dell'esercizio 20.5 Sia ![]() un grafo connesso con
un grafo connesso con ![]() vertici, indichiamo con
vertici, indichiamo con ![]() il numero di
foglie di
il numero di
foglie di ![]() .
Se
.
Se ![]() allora il numero di foglie è esattamente
allora il numero di foglie è esattamente ![]() . Se
. Se ![]() proviamo
che allora il numero di foglie è
proviamo
che allora il numero di foglie è ![]() . Lo proviamo per induzione su
. Lo proviamo per induzione su
![]() . Se
. Se ![]() si vede facilmente, analizzando tutti i grafi connessi con
si vede facilmente, analizzando tutti i grafi connessi con ![]() vertici (sono solo 2) che il massimo numero di foglie è
vertici (sono solo 2) che il massimo numero di foglie è ![]() (uno ne ha
(uno ne ha ![]() e
l'altro non ne ha). Supponiamo la tesi vera per
e
l'altro non ne ha). Supponiamo la tesi vera per ![]() e sia
e sia ![]() un grafo connesso
con
un grafo connesso
con ![]() vertici. Se
vertici. Se ![]() non ha foglie allora la tesi è vera (
non ha foglie allora la tesi è vera (![]() )
altrimenti sia
)
altrimenti sia ![]() una foglia. Il grafo
una foglia. Il grafo ![]() è connesso, ha
è connesso, ha ![]() vertici e quindi, per ipotesi di induzione,
vertici e quindi, per ipotesi di induzione, ![]() . D'altra parte
. D'altra parte ![]() ha al più una foglia in più di
ha al più una foglia in più di ![]() (il vertice
(il vertice ![]() ) e quindi
) e quindi
Un esempio è dato dal grafo ![]() definito da:
definito da:
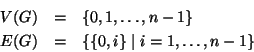
Soluzione dell'esercizio 20.6 Siano ![]() le componenti connesse di
le componenti connesse di ![]() , allora ogni
, allora ogni ![]() è un
albero, ma allora per ogni
è un
albero, ma allora per ogni ![]() si ha
si ha
![]() . Dal fatto
che
. Dal fatto
che
![]() e
e
![]() segue immediatamente la tesi.
segue immediatamente la tesi.
![]()
Soluzione dell'esercizio 21.1 Siano
![]() , allora, dato che
, allora, dato che ![]() è connesso, esiste una
passeggiata
è connesso, esiste una
passeggiata
![]() in
in ![]() che congiunge
che congiunge ![]() a
a ![]() , ossia:
, ossia:
Soluzione dell'esercizio 21.3 Sia ![]() un albero di copertura di
un albero di copertura di ![]() . Chiaramente
. Chiaramente
![]() e
dato che
e
dato che ![]() è un sottografo di
è un sottografo di ![]() allora
allora
![]() e
quindi, usando la formula che lega il numero di lati con il numero dei
vertici di un albero, si ha
e
quindi, usando la formula che lega il numero di lati con il numero dei
vertici di un albero, si ha