Diremo che ![]() è una catena se è totalmente ordinato da
è una catena se è totalmente ordinato da
![]() , ossia se
, ossia se
Un elemento ![]() sarà detto massimale se
sarà detto massimale se
ossia non esiste in
Diremo che ![]() è una catena se è totalmente ordinato da
è una catena se è totalmente ordinato da
![]() , ossia se
, ossia se
Un elemento ![]() sarà detto massimale se
sarà detto massimale se
Enunciamo ora un teorema di cui omettiamo la dimostrazione, ma che è uno degli strumenti più potenti per dimostrare l'esistenza di ``oggetti'' che sono in qualche senso più grandi possibili. Daremo subito nel seguito un'applicazione di tale teorema.
L'unica osservazione che facciamo sulla dimostrazione di questo teorema, è che essa usa im modo sostanziale l'assioma della scelta, anzi si può dimostrare che il lemma di Zorn è equivalente all'assioma della scelta. Si osservi che come l'assioma della scelta anche il lemma di Zorn ha una natura non costruttiva: garantisce l'esistenza di elementi massimali, ma non dà alcuna ``ricetta'' per individuarli.
Dimostrazione.
Consideriamo l'insieme
Definiamo la relazione ![]() su
su ![]() , ponendo per ogni
, ponendo per ogni
![]()
Proviamo che tale ordinamento verifica le ipotesi del lemma di
Zorn. Sia
![]() una catena
e proviamo che ha un maggiorante.
Poniamo
una catena
e proviamo che ha un maggiorante.
Poniamo
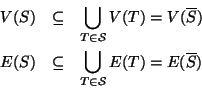
Proviamo nell'ordine che ![]() è un grafo, che è un sottografo di
è un grafo, che è un sottografo di ![]() ,
che è connesso e che non ha cicli.
,
che è connesso e che non ha cicli.
![]() è un grafo. Se
è un grafo. Se
![]() allora esiste
allora esiste
![]() tale che
tale che ![]() . Dato che
. Dato che ![]() è un grafo allora
è un grafo allora
![]() , e dato che
, e dato che
![]() allora
allora
![]() . Quindi
. Quindi
![]() , e per l'arbitrarietà di
, e per l'arbitrarietà di
![]() si ha che
si ha che
![]() .
.
![]() è un sottografo di
è un sottografo di ![]() . Dato che ogni
. Dato che ogni ![]() è
sottografo di
è
sottografo di ![]() , si ha che per ogni
, si ha che per ogni ![]() si ha che
si ha che
![]() e
e
![]() , da cui segue immediatamente che
, da cui segue immediatamente che
![]()
![]() .
.
![]() è connesso. Siano
è connesso. Siano
![]() , allora
esistono
, allora
esistono
![]() tali che
tali che ![]() e
e ![]() . Dato che
. Dato che ![]() è totalmente ordinato da
è totalmente ordinato da ![]() uno tra
uno tra ![]() e
e ![]() è più grande
dell'altro. Supponiamo che sia
è più grande
dell'altro. Supponiamo che sia
![]() . Aallora
. Aallora
![]() e quindi
e quindi ![]() . Dato che
. Dato che ![]() è un albero, esiste un
cammino in
è un albero, esiste un
cammino in ![]() che congiunge
che congiunge ![]() a
a ![]() , sia questo
, sia questo
![]() .
Tale cammino è un cammino anche in
.
Tale cammino è un cammino anche in ![]() dato che per ogni
dato che per ogni ![]() si ha che
si ha che
![]() e
e
![]() .
.
![]() non ha cicli. Supponiamo per assurdo che
non ha cicli. Supponiamo per assurdo che ![]() abbia un ciclo
abbia un ciclo
![]() . Per ogni
. Per ogni ![]()
![]() ,
quindi esiste un
,
quindi esiste un
![]() tale che
tale che ![]() . Usando iterativamente il
fatto che a due a due i
. Usando iterativamente il
fatto che a due a due i ![]() sono uno più grande dell'altro, se ne trova uno
che è più grande di tutti gli altri, ossia esiste
sono uno più grande dell'altro, se ne trova uno
che è più grande di tutti gli altri, ossia esiste ![]() tale che
tale che
![]() per ogni
per ogni ![]() . In modo analogo per ogni lato
. In modo analogo per ogni lato
![]() e quindi per ogni
e quindi per ogni ![]() esiste un
esiste un
![]() tale
che
tale
che
![]() . In modo analogo a quanto fatto sopra si
trova un
. In modo analogo a quanto fatto sopra si
trova un ![]() tale che
tale che
![]() per ogni
per ogni ![]() . Detto infine
. Detto infine ![]() il
più grande tra
il
più grande tra ![]() e
e ![]() si ha che per ogni
si ha che per ogni ![]() si ha che
si ha che
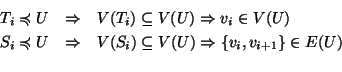
Siamo allora nelle ipotesi per applicare il lemma di Zorn. Sia allora ![]() un elemento massimale.
Quindi
un elemento massimale.
Quindi ![]() è un albero che è un sottografo di
è un albero che è un sottografo di ![]() , massimale rispetto
all'ordinamento
, massimale rispetto
all'ordinamento ![]() . Proviamo che
. Proviamo che ![]() . Per assurdo, sia
. Per assurdo, sia ![]() ma
ma ![]() . Dato che
. Dato che ![]() è connesso (è qui che si usa la
connessione di
è connesso (è qui che si usa la
connessione di ![]() ), preso
), preso ![]() esiste un cammino
esiste un cammino
![]() ,
sia allora
,
sia allora ![]() tale che
tale che
![]() e
e
![]() . Allora il grafo
. Allora il grafo
![]() sarebbe
ancora un elemento di
sarebbe
ancora un elemento di ![]() , sarebbe diverso da
, sarebbe diverso da ![]() e
e
![]() , che
è contro la massimalità di
, che
è contro la massimalità di ![]() .
.
![]()
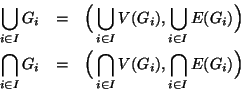
Si provi inoltre che se i ![]() sono tutti connessi e
sono tutti connessi e
![]() per ogni
per ogni ![]() allora
allora
![]() è connesso.
è connesso.
Resta vero l'enunciato precedente se si sostituisce la parola connesso con
![]() -connesso? In caso di risposta negativa si determini l'ipotesi giusta
affinché lo sia.
-connesso? In caso di risposta negativa si determini l'ipotesi giusta
affinché lo sia.
Soluzione