

Next: Lezione 15
Up: Matematica Discreta (II modulo)
Previous: Lezione 13
Subsections
Definizione 14.1
Un grafo
è una coppia ordinata
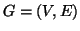
dove
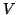
è un insieme non
vuoto detto insieme dei
vertici del grafo ed
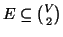
è detto l'insieme dei
lati. Se
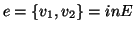
,
si dirà che il lato
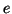 congiunge
congiunge i due vertici
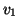
e
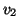
e si
dirà anche che
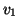
e
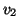
sono gli
estremi del lato
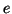
.
Se 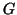 è un grafo, indicheremo con
è un grafo, indicheremo con 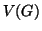 l'insieme dei suoi vertici e con
l'insieme dei suoi vertici e con
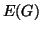 l'insieme dei suoi lati, ovvero
l'insieme dei suoi lati, ovvero
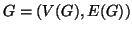 .
.
Se 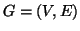 è un grafo e
è un grafo e 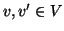 si dirà
che
si dirà
che 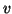 e
e 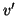 sono adiacenti o che
sono adiacenti o che 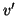 è vicino a
è vicino a 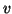 se
se
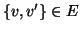 (cfr. esercizio 14.2).
(cfr. esercizio 14.2).
Spesso i grafi sono rappresentati graficamente mediante dei punti a
rappresentare i vertici e delle linee congiungenti due vertici a rappresentare i
lati. Ad esempio in figura 2 sono rappresentati i
grafi 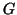 e
e 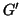 definiti da
definiti da
Figura 2:
Esempi di grafi
 |
Osservazione 14.2
Se
è un grafo, l'essere adiacenti, definisce una relazione su
detta
relazione d'adiacenza che denoteremo con
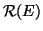
. Ossia:
Tale relazione risulta essere oviamente
- simmetrica ossia
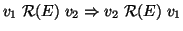
- antiriflessiva ossia
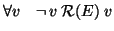
Viceversa, data una relazione simmetrica e antiriflessiva 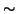 sull'insieme
sull'insieme
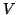 , l'insieme
, l'insieme
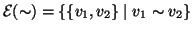 è un sottinsieme
di
è un sottinsieme
di
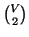 , e quindi
, e quindi
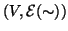 è un grafo.
è un grafo.
Dimostrazione.
(1). Dalle definizioni si ha immediatamente che
e quindi
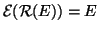 .
.
(2).
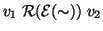 se e solo se
se e solo se
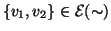 e
per definizione di
e
per definizione di
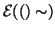 questo è vero se e solo se o
questo è vero se e solo se o
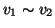 o
o
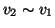 . Dato che la relazione
. Dato che la relazione 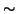 è simmetrica, ciò equivale a
dire
è simmetrica, ciò equivale a
dire
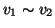 .
.

Osservazione 14.4
La proposizione precedente prova che dare un grafo i cui vertici sono
l'insieme
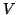
è equivalente a dare una relazione simmetrica e
antiriflessiva su
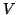
.
Osservazione 14.5
Si osservi che affinchè
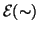
sia l'insieme dei lati di un grafo è
necessario soltanto che
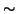
sia antiriflessiva. La simmetria di
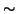
è necessaria però per provare la seconda proprietà della proposizione
precedente.
Esercizio 14.1
Provare nel dettaglio quanto asserito nell'osservazione
14.2.
Soluzione
Esercizio 14.2
Sia
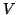
un insieme, e sia
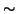
una relazione antiriflessiva su
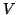
. Si
provi che se
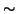
non è simmetrica allora
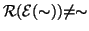
.
Si produca anche un esempio di relazione 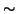 su un insieme tale che
su un insieme tale che
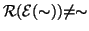 .
.
Soluzione
Definizione 14.6
Un
grafo diretto è una coppia
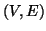
dove
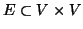
è
una relazione binaria su
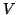
.
Diamo alcuni esempi di grafi notevoli, per i quali esiste anche una notazione
standard.
Per ogni
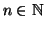 indicheremo con
indicheremo con 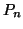 il grafo tale che
il grafo tale che
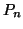 è detto il cammino di lunghezza
è detto il cammino di lunghezza 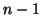 (i.e. ha
(i.e. ha 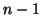 lati).
lati).
Indicheremo con 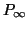 il grafo
il grafo
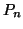 è detto il cammino infinito.
è detto il cammino infinito.
Per ogni
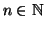 ,
, 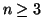 indicheremo con
indicheremo con 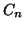 il grafo tale che
il grafo tale che
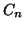 è detto il ciclo di lunghezza
è detto il ciclo di lunghezza 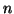 (i.e. ha
(i.e. ha 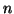 lati e
lati e 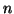 vertici).
vertici).
Per ogni
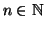 , indicheremo con
, indicheremo con 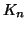 il grafo tale che
il grafo tale che
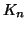 è detto il grafo completo su
è detto il grafo completo su 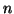 vertici (i.e. ha tutti i lati
possibili che congiungono i suoi
vertici (i.e. ha tutti i lati
possibili che congiungono i suoi 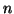 vertici).
vertici).
Per ogni
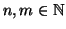 , indicheremo con
, indicheremo con 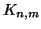 il grafo tale che
il grafo tale che
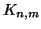 è detto il grafo completo bipartito su
è detto il grafo completo bipartito su 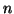 ed
ed 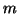 vertici
(i.e. ha tutti i lati possibili che congiungono i suoi primi
vertici
(i.e. ha tutti i lati possibili che congiungono i suoi primi 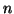 vertici con
gli altri
vertici con
gli altri 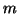 ).
).
Definizione 14.8
Siano
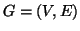
e
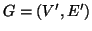
due grafi, si dirà che
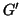
è
sottografo di
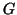
se e solo se
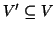
e
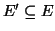
.
Definizione 14.9
Sia
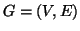
un grafo e sia
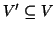
, chiameremo il
sottografo
indotto da
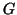
su
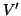
il grafo
![$ G[V']=(V',E\cap {V' \choose 2})$](img1278.gif)
.
Detto in altri termini nel sottografo indotto si mettono tutti i lati del grafo
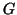 che congiungono vertici di
che congiungono vertici di 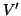 .
.
Esercizio 14.3
Si provi che
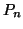
è sottografo di
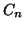
per ogni
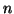
.
Soluzione
Esercizio 14.4
Sia
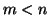
e sia
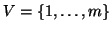
. Si determini il sottografo indotto da
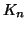
su
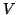
.
Soluzione
Esercizio 14.5
Siano
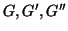
grafi e si provi che se
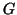
è sottografo di
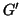
e
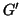
è
sottografo di
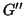
allora
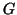
è sottografo di
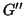
.
Soluzione
Morfismi ed isomorfismo di grafi
Osservazione 14.11
Osserviamo che la condizione di essere un morfismo può essere espressa
anche dicendo che
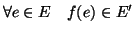
ovvero
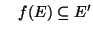
dove con
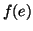
si intende l'immagine mediante

del sottinsieme
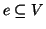
e con
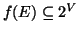
l'insieme di tali immagini al
variare di
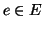
. In simboli
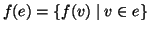
(ovvero se
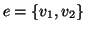
allora
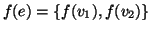
), e
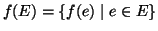
.
Per questo motivo un morfismo sarà denotato anche con
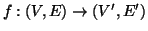 .
.
Osservazione 14.12
Se
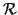
e
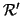
denotano le relazioni di adiacenza dei grafi
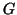
e
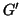
, la
proprietà di essere un morfismo si rienuncia in termini di
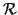
e
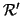
ed in questa forma può essere estesa ai grafi diretti.
Definizione 14.13
Un morfismo
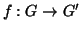
si dice un
isomorfismo se
 è bigettiva
è bigettiva
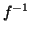 è a sua volta un morfismo.
è a sua volta un morfismo.
In tal caso i due grafi 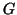 e
e 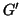 si direnno isomorfi, e si
denoterà con
si direnno isomorfi, e si
denoterà con
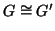 .
.
Proposizione 14.14
Siano
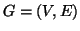
e
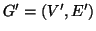
due grafi. Una funzione
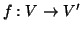
è un
isomorfismo se e solo se
 è bigettiva
è bigettiva
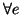
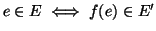 .
.
Dimostrazione.
Supponiamo che  sia un isomorfismo, allora per definizione
sia un isomorfismo, allora per definizione  è
bigettiva. Dal fatto che
è
bigettiva. Dal fatto che  è un morfismo segue che se
è un morfismo segue che se
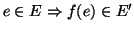 , dal fatto che
, dal fatto che 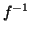 è un morfismo segue allora che se
è un morfismo segue allora che se
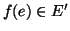 allora
allora
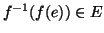 , ma
, ma
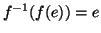 e quindi è verificata la
(2).
e quindi è verificata la
(2).
Viceversa dalla (2) segue che se 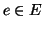 allora
allora
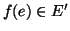 e quindi
e quindi  è
un morfismo. Proviamo che
è
un morfismo. Proviamo che 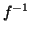 è a sua volta un morfismo. Sia
è a sua volta un morfismo. Sia 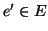 ,
dato che
,
dato che  è bigettiva allora esiste
è bigettiva allora esiste
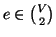 tale che
tale che 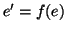 . Ma allora dalla (2) segue che
. Ma allora dalla (2) segue che
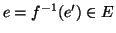 e quindi la tesi.
e quindi la tesi.

Esercizio 14.6
Si provi che
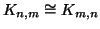
per ogni
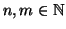
.
Soluzione
Esercizio 14.7
Siano
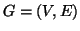
e
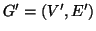
due grafi. Si provi che se
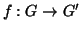
è un
morfismo tale che

è iniettiva e
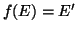
allora

è un isomorfismo.
Soluzione
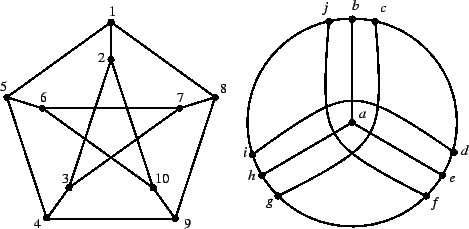
Esercizio 14.9
Si provi che i due grafi rappresentati in figura
4 sono tra
loro isomorfi.
Figura:
I grafi di esercizio 14.9
 |
Soluzione
Esercizio 14.10
Dire se i due grafi in figura
5 sono isomorfi oppure no.
Figura 5:
I grafi dell'esercizio 14.10
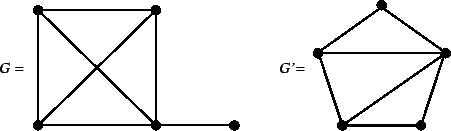 |
Soluzione
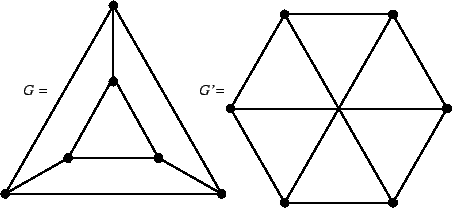
Esercizio 14.11
Provare che i due grafi in figura
6 non sono isomorfi.
Figura 6:
I grafi dell'esercizio 14.11
 |
Soluzione
Esercizio 14.12
Sia
il grafo dato dai vertici e dagli spigoli di un cubo e sia
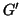
il
grafo tale che
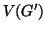
sia l'insieme delle parole di tre lettere nell'alfabeto
di due lettere
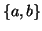
ed in cui due parole sono congiunte da un lato se e
solo se differiscono per una lettera soltanto. Si provi che
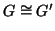
.
Soluzione


Next: Lezione 15
Up: Matematica Discreta (II modulo)
Previous: Lezione 13
Domenico Luminati
2004-03-18
![]() è un grafo e
è un grafo e ![]() si dirà
che
si dirà
che ![]() e
e ![]() sono adiacenti o che
sono adiacenti o che ![]() è vicino a
è vicino a ![]() se
se
![]() (cfr. esercizio 14.2).
(cfr. esercizio 14.2).
![]() e
e ![]() definiti da
definiti da
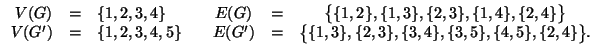
![]() sull'insieme
sull'insieme
![]() , l'insieme
, l'insieme
![]() è un sottinsieme
di
è un sottinsieme
di
![]() , e quindi
, e quindi
![]() è un grafo.
è un grafo.![]() se e solo se
se e solo se
![]() e
per definizione di
e
per definizione di
![]() questo è vero se e solo se o
questo è vero se e solo se o
![]() o
o
![]() . Dato che la relazione
. Dato che la relazione ![]() è simmetrica, ciò equivale a
dire
è simmetrica, ciò equivale a
dire
![]() .
.
![]()
![]() su un insieme tale che
su un insieme tale che
![]() .
.
![]() e
e ![]() di un grafo diretto ci possono essere entrambi i lati
di un grafo diretto ci possono essere entrambi i lati
![]() e
e ![]() , e si possono avere anche lati del tipo
, e si possono avere anche lati del tipo ![]() (vedi
figura 3).
(vedi
figura 3).
![]() anche
anche ![]() ) e antiriflessivo (i.e.
) e antiriflessivo (i.e.
![]() per ogni
per ogni ![]() ). In altri termini la
nozione di grafo diretto è una estensione di quella di grafo.
). In altri termini la
nozione di grafo diretto è una estensione di quella di grafo.![]() indicheremo con
indicheremo con ![]() il grafo tale che
il grafo tale che
![]() il grafo
il grafo
![]() ,
, ![]() indicheremo con
indicheremo con ![]() il grafo tale che
il grafo tale che
![]() , indicheremo con
, indicheremo con ![]() il grafo tale che
il grafo tale che
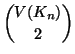
![]() , indicheremo con
, indicheremo con ![]() il grafo tale che
il grafo tale che
![]() .
.![]() e
e ![]() si direnno isomorfi, e si
denoterà con
si direnno isomorfi, e si
denoterà con
![]() .
.![]() sia un isomorfismo, allora per definizione
sia un isomorfismo, allora per definizione ![]() è
bigettiva. Dal fatto che
è
bigettiva. Dal fatto che ![]() è un morfismo segue che se
è un morfismo segue che se
![]() , dal fatto che
, dal fatto che ![]() è un morfismo segue allora che se
è un morfismo segue allora che se
![]() allora
allora
![]() , ma
, ma
![]() e quindi è verificata la
(2).
e quindi è verificata la
(2).
![]() allora
allora
![]() e quindi
e quindi ![]() è
un morfismo. Proviamo che
è
un morfismo. Proviamo che ![]() è a sua volta un morfismo. Sia
è a sua volta un morfismo. Sia ![]() ,
dato che
,
dato che ![]() è bigettiva allora esiste
è bigettiva allora esiste
![]() tale che
tale che ![]() . Ma allora dalla (2) segue che
. Ma allora dalla (2) segue che
![]() e quindi la tesi.
e quindi la tesi.
![]()