Soluzione di alcuni degli esercizi proposti

Soluzione dell'esercizio 1.1 Proviamo la prima. Bisogna provare che $\forall x \quad x\in\varnothing \Rightarrow x\in X$. Ma questo è vero per quanto osservato in 1.4.

A titolo di esempio un po' più significativo, proviamo anche la quarta. Se $X=Y$, allora per il punto 1, si ha che valgono le due inclusioni. Viceversa, supponiamo che valgano le due inclusioni. Dalla prima, per definizione di inclusione ne segue che per ogni $z$, $z \in X \Rightarrow z \in Y$, dalla seconda inclusione in modo analogo segue che per ogni $z$, $z \in Y \Rightarrow z \in X$. Ma allora per ogni $z$, $z \in X \iff z \in Y$, e quindi, per estensionalità ne segue che $X=Y$.     

Soluzione dell'esercizio 1.3 Proviamo la prima delle leggi di De Morgan. $x \in X \setminus (Y \cup Z)$ se e solo se $x\in X$ e $x \not\in Y \cup Z$. Ma ora, dato che $x \in Y \cup Z$ se solo se $x\in Y$ o $x\in Z$, allora $x \not\in Y \cup Z$ se e solo se $x\not\in Y$ e $x\not\in Z$. In definitiva

$$x \in X \setminus (Y \cup Z) \iff x\in X x\not\in Y x\not\in Z.$$ (12)

D'altra parte $x\in (X \setminus Y) \cap (X \setminus Z)$ se e solo se $x\in (X \setminus Y)$ e $(X \setminus Z)$ ossia se solo se $x\in X$ e $x\not\in Y$ e $x\in X$ e $x\not\in Z$, e quindi

$$x \in (X \setminus Y) \cap (X \setminus Z) \iff x\in X x\not\in Y x\not\in Z.$$ (13)

da 24 e 13 assieme all'assioma di separazione segue allora la tesi.     

Soluzione dell'esercizio 1.4 

    

Soluzione dell'esercizio 1.5 Se $f=g$ allora per estensionalità, per ogni $(x,y)\in X\times Y$ $(x,y)\in f$. Ma allora se $x\in X$ allora $(x,f(x))\in f=g$, e quindi $(x,f(x))\in g$, da cui $f(x)=g(x)$.

Viceversa se $(x,y)\in f$ allora $y=f(x)$, ma allora $y=g(x)$ e quindi $(x,y)\in f$, pertanto $f \subseteq g$. Allo stesso modo si prova che anche $g\subseteq f$ e quindi si ha la tesi,     

Soluzione dell'esercizio 1.6 Osserviamo che $X\times \varnothing$ e $\varnothing \times X$ sono entrambi uguali a $\varnothing$. Questo perché per definixione $X \times \varnothing =\{(x,y)\mid x\in X$    e $y\in\varnothing \}$, ma per ogni $y$ $y\not\in\varnothing$.     

Soluzione dell'esercizio 1.7 $f$ è iniettiva. Siano $x_1$ e $x_2\in X$ tali che $f(x_1)=f(x_2)$, allora $g(f(x_1))=g(f(x_2))$ ovvero $g\circ f(x_1)=g\circ f(x_2)$. Dato che $g\circ f= {\rm id}_X$, $g\circ f(x_1)=x_1$ e $g\circ f(x_2) = x_2$ e quindi $x_1=x_2$.

$f$ è suriettiva. Sia $y\in Y$, allora $g(y)\in X$ è tale che $f(g(x))=y$, dato che $f(g(x)) = f \circ g (y) = {\rm id}_Y(y)=y$.     

Soluzione dell'esercizio 1.8  Per definizione, una funzione $f:X\to Y$ è un sottinsieme di $X\times Y$ che verifica la proprietà

$$P(f) := \forall x \in X \quad \exists$$    unico $$y \in Y : (x,y) \in f$$

ossia la collezione di tutte le funzioni da $X$ in $Y$ può essere descritta da:

$$Y^X = \{f\mid f \in 2^{X\times Y}$$    e $$P(f)\}$$

Dato che $X$ e $Y$ sono insiemi allora $X\times Y$ è un insieme. Ma allora anche $2^{X\times Y}$ è un insieme e quindi, per l'assioma di separazione, anche $Y^X$ è un insieme.     

Soluzione dell'esercizio 1.9 

    

Soluzione dell'esercizio 1.10 

    

Soluzione dell'esercizio 1.11 Proviamo la prima delle due. Per definizione di immagine inversa di un insieme, $x\in f^{-1}(\bigcap_{i\in I} A_i)$ se e solo se $f(x)\in \bigcap_{i\in I} A_i$ e questo, per definizione di intersezione, equivale a dire che $f(x) \in A_i$ per ogni $i\in I$, ovvero che $x\in f^{-1}(A_i)$ per ogni $i\in I$, che equivale a dire che $x\in\bigcap_{i\in I} f^{-1}(A_i)$. Si conclude per l'assioma di estensionalità.

Del tutto analoga è la dimostrazione della seconda delle due. $x\in f^{-1}(\bigcap_{i\in I} A_i)$ se e solo se $f(x)\in \bigcup_{i\in I} A_i$ e questo, per la proprietà che caratterizza l'unione, equivale a dire che esiste $i\in I$ tale che $f(x) \in A_i$, ovvero che esiste $i\in I$ tale che $x\in f^{-1}(A_i)$, che equivale a dire che $x\in\bigcup_{i\in I} f^{-1}(A_i)$. Si conclude, anche in questo caso, per l'assioma di estensionalità.     

Soluzione dell'esercizio 1.12 Proviamo soltanto che nella seconda delle due non si ha in generale uguaglianza. Per fare questo, basta dare un esempio, Sia $X=\{0,1\}$, $Y=\{0\}$ e $f:X\to Y$ l'unica funzione possibile. Sia $A_i=\{i\}$ con $i\in \{),1\}$, allora chiaramente $\wedge _0\cap A_1=\varnothing$ e quindi $f(A_0\cap A_1)=\varnothing$. D'altra parte $f(A_i)=\{0\}$ e quindi $f(A_0)\cap f(A_1)=\{0\}$. Chiaramente questo esempio si generalizza con ogni funzione non iniettiva.     

Soluzione dell'esercizio 2.1 Proviamo la seconda. Supponiamo dapprima che $f$ e $g$ siano iniettive; se $f\times g(x,y)=f\times g(x',y')$, allora per definizione di $f\times g$, si ha che $(f(x),g(y)) = (f(x'),g(y;))$, e quindi per definizione di prodotto cartesiano, $f(x)=f(x')$ e $g(y)=g(y')$. Dato che $f$ e $g$ sono entrambe iniettive, questo vuol dire che $x=x'$ e $y=y'$, ovvero che $(x,y)=(x',y')$.

Viceversa, supponiamo che $f\times g$ sia iniettiva; siano $x$, $x'\in X$, tali che $f(x)=f(x')$, allora, prendiamo $y\in Y$ (esiste perché $Y\ne\varnothing$), allora $(f(x),g(y))=(f(x'),g(y))$, ovvero $f\times g(x,y)=f\times g(x',y)$ e quindi $(x,y)= (x',y)$, da cui $x=x'$, ovvero $f$ è iniettiva. In modo del tutto analogo si prova che anche $g$ è iniettiva.

Nel caso che uno dei due insiemi $X$, $Y$ sia vuoto, potrebbe succedere che la funzione prodotto sia iniettiva (o suriettiva) senza che lo sia una delle due funzioni $f$, $g$. Mostriamo questo fatto con due esempi.

Esempio 1.  Si consideri $X=\varnothing$, $Y=\{1,2\}$, $X'=Y'=\{1\}$ e $f$ e $g$ le uniche funzioni possibili, ovvero $f=\varnothing$ e $g(y)=1$, per ogni $y\in Y$. Chiaramente la funzione $g$ non è iniettiva, mentre la funzione prodotto è la funzione vuota ( $f\times g = \varnothing$), che è quindi iniettiva.

Esempio 2.  Si consideri $X=\varnothing$, $Y=\{1\}$, $X'=\varnothing$, $Y'=Y'=\{1,2\}$, $f=\varnothing$ la funzione vuota e $g$ la funzione definita da $g(1)=1$. Chiaramente la funzione $g$ non è suriettiva, mentre la funzione prodotto è la funzione vuota ( $f\times g = \varnothing : \varnothing \to \varnothing$), che è suriettiva.

Le altre due implicazioni restano invece vere anche se $X$ e $Y$ sono vuoti.     

Soluzione dell'esercizio 2.2 Se $A\subseteq X$ definiamo la funzione $\chi_A:X \to \{0,1\}$, ponendo

$$\chi_A(x) = \Big\langle \begin{array}{lcl} 1 &&\text{ se } x\in A [5pt] 0 &&\text{ se } x\not\in A \end{array}$$

Questa funzione viiene chiamata funzione caratteristica o indicatrice di $A$.

Consideriamo la funzione $\Phi:2^X \to \{0,1\}^X$ definita ponendo $\Phi(A)=\chi_A$, e proviamo che $\Phi$ è una bigezione.

$\Phi$ è iniettiva. Dalla definizione di $\chi_A$ si ha immediatamente che $A=\{x\mid \chi_A(x)=1\}$. Per tanto, se $\chi_A=\chi_B$ allora

$$A = \{x\mid \chi_A(x)=1\} = \{x\mid \chi_B(x)=1\} =B.$$

$\Phi$ è suriettiva. Sia $\lambda : X \to \{0,1\}$. Se prendiamo $A=\{x\mid \lambda(x)=1\}$, allora $\chi_A = \lambda$. Infatti per definizione di $A$ si ha che $\lambda(x)=1$ se e solo se $x\in A$, e quindi, poiché $\lambda$ assume valori solo in $\{0,1\}$, se $x\notin A$, necessariamente $\lambda(x)=0$. Ma allora $\lambda$ assume gli stessi valori di $\chi_A$ e quindi coincide con $\chi_A$.     

Soluzione dell'esercizio 2.3 Sia $\Phi : X^{\{0,1\}} \to X\times X$ definita da $\varphi (f)=(f(0),f(1))$ e sia $\Psi : X \times X \to X^{\{0,1\}}$ definita ponendo $\Psi(x_0,x_1)$ la funzione tale che

$$\Psi(x_0,x_1)(0) = x_0$$

$$\Psi(x_0,x_1)(1) = x_1$$

Chiaramente $\Psi\circ \Phi(f) = \Psi(f(0),f(1)$ è, per definizione di $\Psi$, la funzione che in 0 vale $f(0)$ e in $1$ vale $f(1)$, quindi coincide con $f$,

D'altra parte $\Phi\circ\Psi(x_0,x_1)=(\Psi(x_0,x_1)(0),\Psi(x_0,x_1)(1))=(x_0,x_1)$. Ma allora per l'esercizio 1.7, $\Phi$ e $\Psi$ sono bigezioni una inversa dell'altra, da cui la tesi.     

Soluzione dell'esercizio 2.4 Definiamo $\Phi : (X^Y)^Z \to X^{Y\times Z}$ nel seguente modo: se $f \in (X^Y)^Z$, e $(y,z)\in Y\times Z$ poniamo

$$\Phi(f)(y,z)=f(z)(y).$$

Quello che abbiamo scritto ha perfettamente senso, dato che $f(z)$ è una funzione $Y\to X$, ha senso quindi calcolarla in $y$ ed il risultato è un elemento di $X$.

Definiamo ora $\Psi : X^{Y\times Z} \to (X^Y)^Z$ nel modo seguente: se $g \in X^{Y\times Z}$, poniamo

$$\Psi(g)(z)(y) = g(y,z)$$

ossia, fissato $z$, $\Psi(g)(z)$ è la funzione che calcolata in $y$ dà per risultato $g(y,z)$.

In virtù dell'esercizio 1.7 avremo concluso se proviamo che $\Phi\circ \Psi$ e $\Psi \circ \Phi$ sono entrambe l'identità.

Sia $f \in (X^Y)^Z$ e calcoliamo il valore che assume $\Psi\circ \Phi(f)$. Per definizione di $\Psi$, $\Psi\circ \Phi(f)(z) = \Psi(\Phi(f))(z)$ è la funzione che calcolata in $y$ vale $\Psi\circ \Phi(f)$. Per definizione di $\Psi$, $\Psi\circ \Phi(f)(z)(y) = \Phi(f)(y,z)$, e quest'ultimo, per definizione di $\Phi$ coincide con $f(z)(y)$. Ma allora per ogni $z$ $\Psi\circ \Phi(f)(z)=f(z)$, ossia $\Psi\circ \Phi(f)=f$

Se $g \in X^{Y\times Z}$ allora, per definizione di $\Phi$, $\Phi\circ\Psi(g)(y,z)=\Phi(\Psi(g))(y,z)=\Psi(g)(z)(y)$, che a sua volta, per definizione di $\Psi$, è uguale a $g(y,z)$, qualsiasi sia $(y,z)]\in Y\times Z$. Questo basta per dire che $\Phi\circ\Psi(g)=g$.     

Soluzione dell'esercizio 2.5 Consideriamo la funzione $\Phi:X^{Y\cup Z} \to X^Y\times X^Z$ definita da

$$\Phi(f)=(\setbox\restrictbox=\hbox{$\hbox{$f$}_{Y}$}\setbox0\hbox... ...tbox depth\dp\restrictbox \hbox{\vrule depth\dp0 height \ht0 width0pt}_{Z}})$$

Per provare che $\Phi$ è una bigezione, troviamo direttamente la sua inversa. Consideriamo $\Psi : X^Y\times X^Z \to\Phi:X^{Y\cup Z}$ definita da

$$\Psi(g_1,g_2) (x) = \Big \langle \begin{array}{lcl} g_1(x) &&\text{se } x\in Y [5pt] g_2(x) &&\text{se } x\in Z \end{array}$$

Osserviamo innanzitutto che $\Psi(g_1,g_2)$ è ben definita, dato che $Y\cap Z=\varnothing$, e quindi non ci sono ambiguità su quale delle due scegliere per calcolare il valore in $x$. $\Psi(g_1,g_2)$ non è altro che l'unione $g_1 \cup g_2$ (cfr Esempio 1.14), che in questo caso è ben definita dato che $\restriction{g_1}{Y\cap Z}=\restriction{g_2}{Y\cap Z}=\varnothing$.

È immediato verificare che $\Phi\circ \Psi$ $\Psi \circ \Phi$ sono entrambe l'identità.     

Soluzione dell'esercizio 3.1 Proviamo la prima. Procediamo per induzione su $n$. Se $n=0$, per definizione $0+0=0$. Supponiamo la tesi vera per $n$. Allora

$$0 + \mathop{\rm succ}\nolimits (n) = \mathop{\rm succ}\nolimits (0+n) = \mathop{\rm succ}\nolimits (n)$$

dove la prima uguaglianza segue dalla definizione ricorsiva di $+$ e la seconda dall'ipotesi di induzione. Questo prova la tesi.

Proviamo ora la seconda. Per induzione su $n$. Se $n=0$, $1+0=1=succ(0)=0+1$ (per quanto visto nell'osservazione 3.2). Supponiamo la tesi vera per $n$, allora

$$1 + \mathop{\rm succ}\nolimits (n) = \mathop{\rm succ}\nolimits (... ...nolimits (\mathop{\rm succ}\nolimits (n)) = \mathop{\rm succ}\nolimits (n) + 1$$

dove la prima uguaglianza segue dalla definizione ricorsiva di $+$, la seconda dall'ipotesi di induzione ed infine la terza e la quarta da quanto visto nell'osservazione 3.2).     

Soluzione dell'esercizio 3.2 Proviamo soltanto l'associatività della somma. Dobbiamo provare che per ogni $n,m,k\in\mathbb{N}$ si ha che $(n+m)+k=n+(m+k)$. Procediamo per induzione su $k$. Se $k=0$ dalla definizione si ha $(n+m)+ 0 =n+m$ e anche $n+(m+0)=n+(m)=n+m$. Supponiamo la tesi vera per $k$ e proviamola per $\mathop{\rm succ}\nolimits (k)$.

$$(m+n)+\mathop{\rm succ}\nolimits (k) = \mathop{\rm succ}\nolimits ((m+n)+k) = \mathop{\rm succ}\nolimits (m+(n+k)) =$$

$$m+\mathop{\rm succ}\nolimits (n+k)=m+(n+\mathop{\rm succ}\nolimits (k))$$

    

Soluzione dell'esercizio 3.3 Proviamo la prima. $k\le h$, quindi per la prima delle proprietà di proposizione 3.9, si ha $h+m\le h+m$. Per lo stesso motivo anche $n+k\le m +k$. Ma allora per la proprietà commutativa della somma

$$n+k \le m+k = k +m \le h +m = m+ h.$$

Proviamo la seconda. Chiaramente la tesi è vera se $k=0$ o se $n=0$. Supponiamo allora $k\ge1$ e $n \ge 1$ (in particolare anche $m\ge1$), allora

$$nk \le mk = km \le hm = mh$$

che è la tesi,     

Soluzione dell'esercizio 4.2 Siano $f:X\to I_n$ e $g : Y \to I_n$ due bigezioni, allora l'applicazione $h:I_{n+m}\to X\cup Y$ definita da

$$h(i)=\Big\langle \begin{array}{lcl} f(i) &&\text{se } i<n \\ g(i-n) && \text{se } n\le i < m+n \end{array}$$

è una bigezione.

Per la seconda parte si osservi innanzitutto che $X= (X-Y)\cup (X\cap Y)$ e che $(X-Y)\cap (X\cap Y)=\varnothing$ e che quindi per l'esercizio precedente,

$$\left\vert X\right\vert = \left\vert X-Y\right\vert + \left\vert X\cap Y\right\vert$$

osserviamo inoltre che $X\cup Y=(X-Y)\cup Y$ con $(X-Y)\cap Y=\varnothing$ e quindi $\left\vert X\cup Y\right\vert= \left\vert X-Y\right\vert+ \left\vert Y\right\vert$, da cui

$$\left\vert Y\right\vert=\left\vert X\cup Y\right\vert - \left\vert X-Y\right\vert$$

sommando queste due relazioni si ottiene la tesi.     

Soluzione dell'esercizio 4.3 Procediamo per induzione su $n$. Se $n=1$ non c'è nulla da dimostrare. Supponiamo la tesi vera per $n$, usando l'associatività dell'unione si ha

$$\bigcup_{i=1}^{n+1} X_i= ( \bigcup_{i=1}^{n} X_i )\cup X_{n+1}$$

e dato che gli $X_i$ sono a due a due disgiunti, anche $( \bigcup_{i=1}^{n} X_i )\cap X_{n+1}=\varnothing$, ma allora per l'esercizio precedente, e l'ipotesi di induzione, si ha che

$$\left\vert\bigcup_{i=1}^{n+1} X_i\right\vert= \left\vert\bigcup_{... ...t\vert+\left\vert X_{n+1}\right\vert=\sum_{i+1}^{n+1}\left\vert X_i\right\vert$$

    

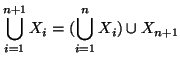
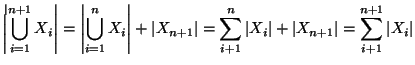
Soluzione dell'esercizio 4.4 Dimostriamo 1. Osserviamo che

$$X \times Y = \bigcup_{x\in X} \{x\}\times Y$$

chiaramente se $x_1\ne x_2$ allora $(\{x_1\}\times Y)\cap(\{x_2\}\times Y)=\varnothing$ e quindi, per l'esercizio precedente,

$$\left\vert X\times Y\right\vert= \left\vert\bigcup_{x\in X} \{x\}\times Y\right\vert = \sum_{x\in X} \left\vert\{x\}\times Y\right\vert.$$

D'altra parte, per ogni $x\in X$ si ha che la funzione $Y\to \{x\}\times Y$ definita da $y\to (x,y)$ è una bigezione, e quindi $\left\vert\{x\}\times Y\right\vert=\left\vert Y\right\vert$, pertanto

$$\left\vert X\times Y\right\vert=\sum_{x\in X} \left\vert Y\right\vert = \left\vert X\right\vert\left\vert Y\right\vert.$$

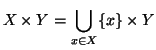
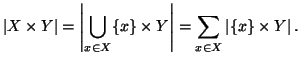
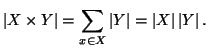
Dimostriamo 2. Procediamo per induzione su $\left\vert X\right\vert$, Se $\left\vert X\right\vert=0$ allora $X=\varnothing$ e $Y^X=\{\varnothing \}$ e quindi $\left\vert X^Y\right\vert=1=\left\vert Y\right\vert^0$, Supponiamo la tesi vera per $\left\vert X\right\vert=n$ e proviamo la tesi quando $\left\vert X\right\vert = n+1$. Fissato un elemento $x_0\in X$, per ogni $y\in Y$ indichiamo con $\mathcal{F}_{x_0,y}=\{f:X\to Y\mid f(x_0)=y\}$. Osserviamo che evidentemente

$$Y^X = \bigcup_{y\in Y} \mathcal{F}_{x_0,y}$$

e d'altra parte per ogni $y_1\ne y_2$ si ha $\mathcal{F}_{x_0,y_1}\cap\mathcal{F}_{x_0,y_2} = \varnothing$, quindi

$$\left\vert Y^X\right\vert=\sum_{y\in Y}\left\vert\mathcal{F}_{x_0,y}\right\vert.$$

Ma ora, detto $X'=X-\{x_0\}$, osserviamo che per ogni $y\in Y$, l'insieme $\mathcal{F}_{x_0,y}$ è in bigezione con $Y^{X'}$, ad esempio mediante la funzione $\Phi:\mathcal{F}_{x_0,y}\to Y^{X'}$ definita da $f\to \setbox\restrictbox=\hbox{$\hbox{$f$}_{X'}$}\setbox0\hbox{$f$} {{f} \vru... ...ctbox depth\dp\restrictbox \hbox{\vrule depth\dp0 height \ht0 width0pt}_{X'}}$. Ma allora

$$\left\vert Y^X\right\vert=\left\vert Y\right\vert\left\vert Y^{X'}\right\vert.$$

Per concludere, osserviamo che $\left\vert X'\right\vert=\left\vert X\right\vert-1=n$ e quindi, per ipotesi di induzione $\left\vert Y^{X'}\right\vert=\left\vert Y\right\vert^n$ e quindi

$$\left\vert Y^X\right\vert=\left\vert Y\right\vert\left\vert Y\rig... ...t\vert Y^{n+1}\right\vert = \left\vert Y\right\vert^{\left\vert X\right\vert}.$$

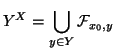
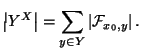
Il terzo punto dell'esercizio segue allora dal secondo e dall'esercizio 2.2.     

Soluzione dell'esercizio 4.5 Indichiamo con $\mathcal{I}(X,Y)$ l'insieme delle funzioni iniettive $X\to Y$. Procediamo per induzione su $k$. Se $k=0$ allora $X=\varnothing$ e quindi $Y^X=\{\varnothing \}$ e la funzione $\varnothing :\varnothing \to Y$ è iniettiva. Quindi $\mathcal{I}(\varnothing ,Y)=\{\varnothing \}$ ha cardinalità $1=n!/(n-0)!$.

Supponiamo la tesi vera per $k$ e proviamola per $k+1$. Supponiamo quindi che $\left\vert X\right\vert=k+1\le \left\vert Y\right\vert$. Chiaramente $X\ne\varnothing$ e quindi esiste un elemento $x_0\in X$. Consideriamo per ogni $y\in Y$ l'insieme

$$\mathcal{I}_y = \{f\in \mathcal{I}(X,Y) \mid f(x_0)=y\}.$$

Si ha evidentemente che

$$\mathcal{I}(X,Y)=\bigcup_{y\in Y} \mathcal{I}_y$$

e per ogni $y_1\ne y_2$ $\mathcal{I}_{y_1}\cap \mathcal{I}_{y_2}=\varnothing$. Quindi

$$\left\vert\mathcal{I}(X,Y)\right\vert = \sum_{y\in Y} \left\vert\mathcal{I}_y\right\vert$$

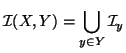
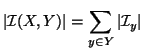
Osserviamo ora che $\mathcal{I}_y$ è in bigezione con $\mathcal{I}(X\setminus\{x_0\} , Y\setminus\{y\})$ quindi, visto che $\left\vert X\setminus\{x_0\}\right\vert=k$ e $\left\vert Y\setminus\{y\}\right\vert=n-1$, per ipotesi di induzione, si ha che $\left\vert\mathcal{I}(X\setminus\{x_0\} , Y\setminus\{y\})\right\vert=(n-1)!/(n-1-k)!$.

Ma allora

$$\left\vert\mathcal{I}(X,Y)\right\vert = \sum_{y\in Y} \left\vert\mathcal{I}(X\setminus\{x_0\} , Y\setminus\{y\})\right\vert$$

$$= \sum_{y\in Y} \frac{(n-1)!}{(n-1-k)!} = n \frac{(n-1)!}{(n-1-k)!}= \frac{n!}{(n-(k+1))!}$$

    

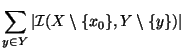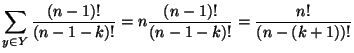Soluzione dell'esercizio 4.6 Sia $f:X\to Y$ iniettiva. Se $Y'$ è l'immagine di $f$ allora $f:X\to Y'$ è evidentemente surgettiva e quindi bigettiva. Ma allora $X\sim Y'$ e quindi $\left\vert X\right\vert=\left\vert Y'\right\vert\le \left\vert Y\right\vert = \left\vert X\right\vert$. Ma allora necessariamente $Y'=Y$, ovvero $f$ è surgettiva.     

Soluzione dell'esercizio 4.7 Per l'esercizio precedente, l'insieme delle bigezioni di $X$ in sé coincide con l'insieme delle funzioni iniettive $X\to X$ e quindi, si può usare la formla dell'esrcizio 4.5, che nel caso $k=n$ dà $n!/0!=n!/1=n!$.     

Soluzione dell'esercizio 5.1  Se una tale $g$ esiste, $f$ è surgettiva, dato che per ogni $y\in Y$ si ha che $f(g(y))=y$.

Viceversa, supponiamo che $f$ sia surgettiva, allora $f^{-1}(y)\ne\varnothing$ per ogni $y\in Y$, per l'assioma di scelta, esiste una funzione di scelta, $g:Y\to\bigcup_{y\in Y}f^{-1}(y)$, tale che $g(y)\in f^{-1}(y)$ per ogni $y\in Y$, ma ciò significa che $f(g(y))=y$ per ogni $y\in Y$, ossia che $g$ è una inversa destra di $f$.     

Soluzione dell'esercizio 5.2 Se una tale $g$ esiste allora $f$ deve necessariamente essere iniettiva, infatti se $f(x_1)=f(x_2)$ allora $x_1=g(f(x_1))=g(f(x_2))x_2$.

Viceversa, supponiamo che $f$ sia iniettiva. Allora per ogni $y\in f(X)$ esiste un unico $x_y\in X$ tale che $f(x_y)=y$. Preso un arbitrario $\overline{x}\in X$ definiamo $g:Y\to X$ ponendo

$$g(y)=\Big\langle \begin{array}{lcl} x_y &&\text{se }y\in f(X) \\ \overline{x} &&\text{se }y\notin f(X) \end{array}$$

Dato che per ogni $x\in X$ l'unico elemento avente $f(x)$ come immagine è $x$ stesso, si ha che $g(f(x))=x$.     

Soluzione dell'esercizio 5.3 

    

Soluzione dell'esercizio 6.1 

    

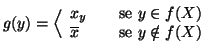
Soluzione dell'esercizio 6.2 A partire dagli $X_m$ costruiamo dei nuovi insiemi, ponendo

$$Y_0 = X_0$$

$$Y_{n+1} = X_{n+1} - \bigcup_{m=0}^{n} X_m \qquad \forall n \ge 0$$

Gli insiemi in questione sono a due a due disgiunti, e $\bigcup_nY_n=\bigcup_nX_n$. Si consideri l'insieme $A=\{n\in\mathbb{N}\mid Y_n\ne\varnothing \}$, allora $Y=\bigcup_{n\in A}Y_n$. Per quanto visto in precedenza $A$ è finito o numerabile. Nel primo caso $A$ è finito, nel secondo caso è numerabile.     

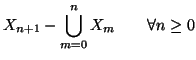Soluzione dell'esercizio 6.3 Come nell'esercizio precedente, poniamo

$$Y_0 = X_0$$

$$Y_{n+1} = X_{n+1} - \bigcup_{m=0}^{n} X_m \qquad \forall n \ge 0$$

Gli insiemi in questione sono a due a due disgiunti, e $\bigcup_nY_n=\bigcup_nX_n$. Si consideri l'insieme $A=\{n\in\mathbb{N}\mid \left\vert Y_n\right\vert=\aleph_0\}$, $B=\{n\in\mathbb{N}\mid Y_n\ne\varnothing$    ed è finito$\}$, allora $Y=\bigcup_{n\in A}Y_n\cup\bigcup_{n\in B}Y_n$. Per quanto visto in precedenza $A$, e $B$ sono finiti o numerabili. Dato che $Y_0$ è numerabile, $A\ne\varnothing$ e quindi $\bigcup_{n\in A}Y_n$ è numerabile. D'altra parte $\bigcup_{n\in B}Y_n$ è finito o numerabile e quindi la loro unione è numerabile.     

Soluzione dell'esercizio 6.4 

    

Soluzione dell'esercizio 6.5 

    

Soluzione dell'esercizio 6.6 

    

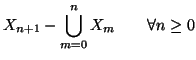Soluzione dell'esercizio 6.7 La funzione $f:(0,1)\to\mathbb{R}$ definita da $f(t)=\tan(\pi t-\pi/2)$ è una bigezione.     

Soluzione dell'esercizio 6.8 Osserviamo che $X-Y$ non può essere né finito né numerabile, altrimenti $X=(X-Y)\cup Y$ sarebbe numerabile. Ma allora $X-Y$ contiene un sottinsieme, $Y'$, numerabile. Dato che $Y$ e $Y'$ sono entrambi numerabili, la loro unione è numerabile, sia quindi $f:Y'\to Y\cup Y'$ una bigezione e si definisca $g:X-Y\to X$ ponendo:

$$g(x)=\Big\langle \begin{array}{lcl} f(x) &&\text{se } x\in Y' \\ x &&\text{se } x\in X-(Y\cup Y') \end{array}$$

$g$ è chiaramente una bigezione.     

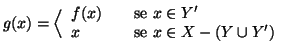
Soluzione dell'esercizio 6.9 Per ogni $k\in\mathbb{N}$ sia $F_k=\{A\in 2^\mathbb{N}\mid \left\vert A\right\vert = k\}$. Chiaramente $F=\bigcup_{k\in\mathbb{N}}F_k$. Proviamo che $\left\vert F_k\right\vert=\aleph_0$ per ogni $k\ge1$. Procediamo per induzione su $k$. Se $k=1$ allora l'applicazione $n\to \{n\}$ è una bigezione $\mathbb{N}\to F_1$. Supponiamo che $F_k$ sia numerabile, allora per ogni $A\in F_k$ sia $F_{k+1}(A)=\{B\in F_{k+1}\mid B\supseteq A\}$. per ogni $A$ l'insieme $F_{k+1}(A)$ è numerabile, in quanto in bigezione con $\mathbb{N}-A$, inoltre $F_{k+1}-\bigcup_{A\in F_k}F_{k+1}(A)$ è numerabile in quanto unione di una famiglia numerabile di insiemi numerabili.     

Soluzione dell'esercizio 6.10 

    

Soluzione dell'esercizio 7.1 

    

Soluzione dell'esercizio 7.2 

    

Soluzione dell'esercizio 7.3 

    

Soluzione dell'esercizio 7.4 

    

Soluzione dell'esercizio 7.5 

    DIVE (n,m) {
      N=n
      M=m
      Q=0
      R=N
      WHILE N > M-1 DO
        N = N-M
        R = N
        Q = Q+1
      END WHILE
    }

    

Soluzione dell'esercizio 8.1 Dalla definizione del coefficiente binomiale si ha

$${n \choose k}+{n \choose k-1} = \frac{n!}{k!(n-k)!}+\frac{n!}{(k-1)!(n-k+1)!} =$$

$$= \frac{n!(n-k+1)+n!k}{(k)!(n-k+1)!} = \frac{n!(n+1)}{(k)!(n-k+1)!} = {n+1 \choose k}$$

    

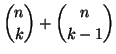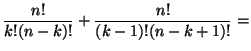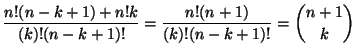Soluzione dell'esercizio 8.2 Si osservi che se $X$ è un insieme con $n$ elementi, allora

$$2^X=\bigcup_{k=0}^n{X \choose k}$$

e che questi insiemi sono a due a due disgiunti. Quindi

$$2^n=2^{\left\vert X\right\vert}=\left\vert 2^X\right\vert=\sum_{k... ...ert= \sum_{k=0}^n{\left\vert X\right\vert \choose k}=\sum_{k=0}^n{n \choose k}$$

    

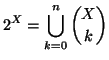
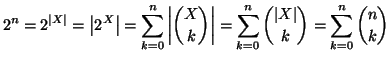
Soluzione dell'esercizio 10.1 Procediamo per induzione su $k$. Se $k=1$ non c'è nulla da dimostrare. Supponiamo che la tesi sia vera per $k$ e supponiamo che $p\mathrel{\big\vert}n_1n_2\dots n_{k+1}$, ossia $p\mathrel{\big\vert}(n_1n_2\dots n_k)n_{k+1}$. Per il corollario 10.2, si ha che $p\mathrel{\big\vert} n_1n_2\dots n_k$ oppure $p\mathrel{\big\vert}n_{k+1}$. Se si verifica la seconda eventualità abbiamo finito, altrimenti, per ipotesi di induzione esiste $i\in \{1,\dots,k\}$ tale che $p\mathrel{\big\vert}n_i$, e quindi si conclude.     

Soluzione dell'esercizio 10.2 

    

Soluzione dell'esercizio 10.3 

    

Soluzione dell'esercizio 10.4 Chiaramente $\prod _{i=1}^s p_i^{k_i\wedge h_i}$ è un divisore comune a $n$ e $m$. Inoltre se $c$ è un divisore comune non può avere fattori primi diversi dai $p_i$, quindi $c=\prod _{i=1}^s p_i^{l_i}$. Dal fatto che $c\mathrel{\big\vert}n$ segue allora che $l_i\le k_i$ e dal fatto che $c\mathrel{\big\vert}m$ segue che $l_i\le h_i$ per ogni $i$, e quindi $l_i\le k_i\wedge h_i$.

La formula per il m.c.m. segue allora dal fatto che $[n,m]=\left\vert nm\right\vert/(n,m)$, e che per ogni coppia di numeri reali si ha che $h+k-h\wedge k=h\vee k$.     

Soluzione dell'esercizio 11.1 Per quanto visto nell'osservazione 11.8, possiamo definire l'applicazione $\Phi:R\to P$ data da $\Phi({\cal R})=X\big/\mathchoice {{}_{\!\displaystyle {}{\cal R}}} {{}_{\!\tex... ...al R}}} {{}_{\!\scriptstyle {}{\cal R}}} {{}_{\!\scriptscriptstyle {}{\cal R}}}$.

Data invece una partizione ${\cal P}\in P$ definiamo la relazione $\stackrel{{\cal P}}{\sim}$ ponendo

$$x_1\stackrel{{\cal P}}{\sim}x_2\iff \exists A\in {\cal P}: x_1,x_2\in A.$$

Proviamo che $\stackrel{{\cal P}}{\sim}$ è una relazione d'equivalenza.

$\stackrel{{\cal P}}{\sim}$ è riflessiva. Se $x\in X$ allora, dato che ${\cal P}$ ricopre $X$ (proprietà (2) di 11.8), esiste $A\in {\cal P}$ tale che $x\in A$ e quindi $x\stackrel{{\cal P}}{\sim}x$.

$\stackrel{{\cal P}}{\sim}$ è simmetrica. Ovvio.

$\stackrel{{\cal P}}{\sim}$ è transitiva. Siano $x_1\stackrel{{\cal P}}{\sim} x_2$ e $x_2\stackrel{{\cal P}}{\sim} x_3$, allora esistono $A,B\in {\cal P}$ tali che $x_1,x_2\in A$ e $x_2, x_3\in B$. Ma, allora $x_2\in A\cap B$ ossia $A\cap B\ne\varnothing$ e quindi coincidono (proprietà (3) di 11.8) ossia $A=B$ e quindi $x_1,x_3\in A$ ovvero $x_1\stackrel{{\cal P}}{\sim} x_3$.

Definiamo allora $\Psi:P\to R$ ponendo $\Psi({\cal P})=\stackrel{{\cal P}}{\sim}$, e proviamo che $\Phi\circ\Psi={\rm id}$ e $\Psi\circ\Phi={\rm id}$. Ciò concluderà la dimostrazione.

Sia ${\cal R}\in R$, allora, per la (2) della proposizione 11.7, si ha che $x_1{\cal R}x_2$ se e solo se $\left[x_1\right]_{{\cal R}}=\left[x_2\right]_{{\cal R}}$ ossia se e solo se esiste $A\in X\big/\mathchoice {{}_{\!\displaystyle {}{\cal R}}} {{}_{\!\textstyle {}{\cal R}}} {{}_{\!\scriptstyle {}{\cal R}}} {{}_{\!\scriptscriptstyle {}{\cal R}}}$ tale che $x_1,x_2\in A$ ossia se e solo se esiste $A\in \Phi({\cal R})$ tale che $x_1,x_2\in A$ ossia se e solo se $x_1\stackrel{\Phi({\cal R})}{\sim} x_2$ e quindi ${\cal R}=\Psi(\Phi({\cal R}))$.

Sia invece ${\cal P}\in P$, allora, dato $A\in P$ sia $x\in A$, è chiaro che $\left[x\right]_{\stackrel{{\cal P}}{\sim}}=A$, ciò unito al fatto che ${\cal P}$ ricopre $X$ (proprietà (2) di 11.8) permette di concludere che $X\big/\mathchoice {{}_{\!\displaystyle {}\stackrel{{\cal P}}{\sim}}} {{}_{\!\t... ...al P}}{\sim}}} {{}_{\!\scriptscriptstyle {}\stackrel{{\cal P}}{\sim}}}={\cal P}$ ovvero che $\Phi(\Psi({\cal P}))={\cal P}$.     

Soluzione dell'esercizio 11.2 Proviamone l'ultima a titolo di esempio, le a ltre si dimostrano in modo completamente analogo.

$$\left[a\right] ( \left[b\right] + \left[c\right]) = \left[a\right... ...\left[ac\right]= (\left[a\right]\left[b\right])+(\left[a\right]\left[c\right])$$

    

Soluzione dell'esercizio 12.1 

    

Soluzione dell'esercizio 12.2 Osserviamo che per ogni $i\in\mathbb{N}$ si ha che $10^i\cong 1\quad{\rm mod} 3$. Questo perché $10 \cong 1 \quad{\rm mod} 3$ e quindi $10^i \cong 1^i=1 \quad{\rm mod} 3$. Ma allora

$$n = \sum _{i=0}^k \varepsilon _i 10^i \cong \sum _{i=0}^k \varepsilon _i \quad{\rm mod} 3$$

quindi $3\mathrel{\big\vert}n$ se e solo se $n\cong 0 \quad{\rm mod} 3$ se e solo se $\sum _{i=0}^k \varepsilon _i\cong 0 \quad{\rm mod} 3$ se e solo se $3\mathrel{\big\vert}\sum _{i=0}^k \varepsilon _i$.

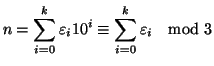
Del tutto analoga è la dimostrazione della seconda. Per quanto riguarda la terza si adatti la dimostrazione della prima osservando che $10\cong -1 \quad{\rm mod} 11$ e quindi

$$10 ^ i \cong (-1)^i = \big\langle \begin{array}{ll} 1 & \text{se } x \text{ \\lq e pari} \\ -1 & \text{se } x \text{ \\lq e dispari} \end{array}$$

    

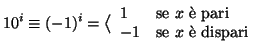
Soluzione dell'esercizio 13.1 Sia $c$ una soluzione di $a x \cong b \quad{\rm mod} n$, allora $n \mathrel{\big\vert}(ac-b)$ ossia $ac - b = kn$. Ma allora $a'(a,n) c -b'(a,n) = kn'(a,n)$ da cui segue che $a'c-b'=kn'$, ossia $c$ è una soluzione della seconda congruenza.

Viceversa se $c$ risolve $a' x \cong b' \quad{\rm mod} n'$ allora esiste $k$ tale che $a'c-b'=kn'$ e quindi $ac-b=(a'c-b')(a,n) = kn'(a,n)=kn$, ossia $c$ risolve la prima congruenza.     

Soluzione dell'esercizio 13.2 Se $y\in\left[x\right]_n$ allora $n\mathrel{\big\vert}(x-y)$, ma dato che $n'\mathrel{\big\vert}n$ allora anche $n'\mathrel{\big\vert}(x-y)$, ovvero $y\in\left[x\right]_{n'}$.

Proviamo innanzitutto che $\left[x+in'\right]_n\subseteq \left[x\right]_{n'}$ per ogni $i$. Infatti se $y\in\left[x+in'\right]_n$ allora $n\mathrel{\big\vert}(x-y+in')$ e quindi $n'\mathrel{\big\vert}(x-y+in')$, da cui segue che $n'\mathrel{\big\vert}(x-y)$ ossia che $y\in\left[x\right]_{n'}$. Da questo fatto ne consegue allora che $\left[x\right]_{n'} \supseteq \bigcup _{i=0}^{d-1}\left[x+in'\right]_n$. Dimostriamo l'inclusione opposta. Sia $y\in\left[x\right]_{n'}$, e sia $r$ il resto della divisione euclidea di $x-y$ per $n$, ossia $x-y=qn+r$ con $0\le r<n$. Allora $n'\mathrel{\big\vert}x-y$ e quindi $n'\mathrel{\big\vert}r$, ovvero esiste $i$ tale che $r=in'$ e $0\le i \le d-1$. Inoltre $x+r-y=nq$ e quindi $y \cong x+r=x+id\quad{\rm mod} n$, ossia $y\in \bigcup_{i=0}^{d-1} \left[x+in'\right]_n$.

Per concludere osserviamo che affinché si abbia $\left[x+in'\right]_n\ne\left[x+jn'\right]_n$ deve aversi $x+in'\cong x+jn'\quad{\rm mod} n$, ovvero $n\mathrel{\big\vert}(i-j)n'$. Supposto per assurdo che $j<i$ si ha allora che $0<i-j<d$ e quindi $0<(i-j)n'<dn'= n$, ma allora $(i-j)n'$ non potrebbe essere un multiplo di $n$.     

Soluzione dell'esercizio 13.3 Osserviamo che $X=\left[x\right]_n$ risolve l'equazione $\left[a\right]_nX=\left[b\right]_n$ se e solo se $a x \cong b \quad{\rm mod} n$. Per l'esercizio 13.1 se $c$ è una soluzione intera allora tutte le soluzioni intere sono $\left[c\right]_{n'}$. Ma allora per l'esercizio precedente $\left[c\right]_{n'}=\bigcup _{i=0}^{(a,n)-1}\left[x+in'\right]_n$ e le classi $\left[x+in'\right]_n$ con $i=0,\dots.(a,n)-1$ sono tutte diverse. Queste sono tutte e sole le soluzioni in $\mathbb{Z}\big/\mathchoice {{}_{\!\displaystyle {}n\mathbb{Z}}} {{}_{\!\textst... ...} {{}_{\!\scriptstyle {}n\mathbb{Z}}} {{}_{\!\scriptscriptstyle {}n\mathbb{Z}}}$ dell'equazione lineare $\left[a\right]_nX=\left[b\right]_n$.     

Soluzione dell'esercizio 13.4 Sia $x\in\mathbb{Z}$ allora o $p\mathrel{\big\vert}x$ oppure $(x,p)=1$, ma nel primo caso $\left[x\right]_p=\left[0\right]_p$ nel secondo caso $\left[x\right]_p$ è invertibile mod $p$ e quindi $\left[x\right]_p^{p-1}=\left[1\right]_p$ ovvero $\left[x\right]_p^{p-1}-\left[1\right]_p=\left[0\right]_p$. Ne consegue che in ogni caso il prodotto di $\left[x\right]_p$ e di $\left[x\right]_p^{p-1}-\left[1\right]_p$ è $\left[0\right]_p$ ovvero

$$\left[0\right]_p = \left[x\right]_p(\left[x\right]_p^{p-1}-\left[1\right]_p)=(\left[x\right]_p\left[x^{p-1}\right]_p-\left[1\right]_p)=$$

$$= \left[x\right]_p\left[x^{p-1}-1\right]_p=\left[x(x^{p-1}-1)\right]_p=\left[x^{p}-x\right]_p$$

quindi $p\mathrel{\big\vert}(x^p-x)$ ovvero $x^p-\cong x \quad{\rm mod} p$.     

Soluzione dell'esercizio 13.5 Osserviamo che $(a,pq)\ne1$ se e solo se $p \mathrel{\big\vert}a$ o $p \mathrel{\big\vert}a$, ma i numeri più piccoli di $pq$ che sono divisibili per $p$ sono $p$, $2p,\dots,qp$, quelli che sono divisibili per $q$ sono invece $q$, $2q,\dots,pq$ e quindi i numeri più piccoli di $pq$ e non coprimi con $pq$ sono $p+q-1$. Quindi $\Phi(pq)=pq-(p+q-1)=(p-1)(q-1)$.     

Soluzione dell'esercizio 13.6  $\Phi(n)=(p-1)(q-1)=pq -p -q +1= n -p -q +1$ da cui $p+q=n+1-\Phi(n)$. Quindi $p$ e $q$ sono determinati dal sistema di equazioni

$$\left\{ \begin{array}{l} p+q=n+1-\Phi(n) \\ pq=n \end{array}\right.$$

Una semplice sostituzione mostra che allora $p$ e $q$ devono essere le due radici dell'equazione $x^2-(n+1-\Phi(n))+n=0$.     

Soluzione dell'esercizio 13.7 

    

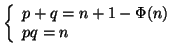
Soluzione dell'esercizio 14.1 La relazione $\mathrel{{\cal R}(E)}$ è simmetrica. Infatti se $v_1\mathrel{{\cal R}(E)}v_2\iff\{v_1,v_2\}\in E$. Ma $\{v_1,v_2\}={v_2,v_1}$, quindi anche $\{v_2,v_1\}\in E$ e quindi $v_2\mathrel{{\cal R}(E)}v_1$.

La relazione $\mathrel{{\cal R}(E)}$ è antiriflessiva. Infatti per ogni $v\in V$ $\{v\}=\{v,v\}\notin E$ e per tanto $\lnot v {\mathrel{{\cal R}(E)}} v$.

Se $\sim$ è antiriflessiva, allora ${\cal E}(\sim)\subseteq {V \choose 2}$, infatti se $e\in{\cal E}(\sim)$ allora, per definizione di ${\cal E}(\sim)$, $e=\{v_1,v_2\}$ con $v_1\sim v_2$, e dato che $\sim$ è antiriflessiva, $v_1\ne v_2$ e quindi $\left\vert e\right\vert =2$ ovvero $e\in {V \choose 2}$ ovvero ${\cal E}(\sim)\subseteq {V \choose 2}$.     

Soluzione dell'esercizio 14.2 Per quanto visto nell'osservazione 14.2, la relazione $\mathrel{{\cal R}({\cal E}(\sim))}$ è sempre simmetrica, quindi non potrà essere uguale a $\sim$ che non lo è.

Un esempio. $X=\{0,1\}$ e $\sim=\{(0,1)\}$. Evidentemente $0\sim1$ ma $1\not\sim 0$.     

Soluzione dell'esercizio 14.4  Il sottografo indotto $K_n[V]$ è isomorfo a $K_m$. Sia $f:\{1,\dots,m\}\to V$ una funzione bigettiva. $f$ è evidentemente un isomorfismo dato che tutte le coppie di elemnti di $\{1,\dots,m\}$ sono lati di $K_m$ e tutte le coppie di eleenti $\{v_1,v_2\}$ al variare di $v_1\ne v_2\in V$ sono lati di $K_n$ e quindi di $K_n[V]$.

Volendo essere più formali, dato che $K_n$ è completo, per ogni $1\le i \ne j \le m$ il lato $\{f(i),f(j)\}\in E(K_n)$ e quindi $\{f(i),f(j)\}\in E(K_n[V])$. D'altra parte se $\{v_1,v_2\}\in E(K_n[V])$, allora esistono $1\le i\ne j m$ tali che $f(i)=v_1$ e $f(j)=v_2$ e dato che $K_m$ è il grafo completo, $\{i,j\}\in E(K_m)$.     

Soluzione dell'esercizio 14.5 

    

Soluzione dell'esercizio 14.6 

    

Soluzione dell'esercizio 14.7 

    

Soluzione dell'esercizio 14.8 

    

Soluzione dell'esercizio 14.9 La colorazione dei lati data in figura 15

Figura 15: Soluzione grafica dell'esercizio 14.9

suggerisce come definire l'isomorfismo. Precismante se si definisce la funzione $f:\{1,2,\dots,10\}\to\{a,b,\dots,j\}$ ponendo

$$\begin{array}{rclcrclcrclcrclcrcl} f(1)&=&a &\quad & f(2)&=&b &\q... ...d & f(7)&=&g &\quad & f(8)&=&h &\quad & f(9)&=&i &\quad & f(10)&=&j \end{array}$$

una semplice verifica mostra che $f$ è un isomorfismo.     

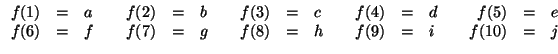
Soluzione dell'esercizio 14.10 

    

Soluzione dell'esercizio 14.11 

    

Soluzione dell'esercizio 14.12 Se identifichiamo la lettera $a$ con il numero 0 e la $b$ con l'$1$, si ottiene una identificazione delle parole con le coordinate dei vertici del cubo di $\mathbb{R}^3$ dato da $[0,1]\times[0,1]\times[0,1]$. Inoltre due vertici di tale cubo sono congiunti da uno spigolo se solo se differiscono esattamente per una coordinata. L'identificazione data è quindi un isomorfismo di grafi tra $G$ e $G'$.

Figura 16: L'isomorfismo tra i grafi dell'esercizio 14.12

    

Soluzione dell'esercizio 16.1  Chiaramente $E(G) \supseteq \bigcup_{i\in I}E(G_i)$. Proviamo l'inclusione opposta. Se $e\in E(G)$ allora $e=\{u,v\}$ ed i vertici $u,v$ sono evidentemente congiungibili. Allora sono vertici di una medesima componente connessa, ovvero esiste $i$ tale che $u,v\in V(G_i)$. Per definizione di componente connessa e di sottografo indotto $e=\{u,v\}\in G_i$. Quindi, per l'arbitrarietà di $u,v\in E$ se ne deduce che $E(G) \subseteq \bigcup_{i\in I}E(G_i)$.     

Soluzione dell'esercizio 16.2 Segue immediatamente dall'esercizio precedente e dall'osservare che gli insiemi dei lati di due componenti diverse sono necessariamente disgiunti.     

Soluzione dell'esercizio 16.3 Siano $u,v\in V(G)=V(G')$, dato che $G'$ è connesso esiste una passeggiata in $G'$ che li congiunge, sia questa $P=(v_0,v_1,\dots,v_n)$. Ossia $\{v_i,v_{i+1}\}\in E(G')$ per ogni $i$. Ma dato che $G'$ è un sottografo di $G$, allora $E(G')\subseteq E(G)$ e quindi $\{v_i,v_{i+1}\}\in E(G)$ per ogni $i$, ossia $P$ è una passeggiata in $G$, quindi $u,v$ sono congiungibili in $G$.     

Soluzione dell'esercizio 19.1 Sia $e=\{x,y\}$ e siano $u,v\in V(G\%e)=V(G)\cup\{z\}$, si hanno due casi:

1. $u \ne z$ e $v\ne z$;
2. $u=z$ oppure $v=z$.

Nel primo caso sia $(u=v_0,v_1,\dots,v_n=v)$ un cammino in $G$ che congiunge $u$ e $v$. Se questo non passa per il lato $e$, allora è un cammino anche in $G\%e$, se invece per qualche $i$ si ha $e=\{v_i,v_{i+1}$ allora basta considerare il nuovo cammino $(v_0,\dots,v_i, z, v_{i+1},\dots,v_n)$ che congiunge $u$ a $v$ in $G\%e$.

Nel secondo caso, supponiamo che $v=z$ allora per il passo precedente sappiamo che $u$ è congiungibile con $x$ in $G\%e$, d'altra parte $x$ è congiungbile con $z$ e quindi $u$ è congiungibile con $z=v$.     

Soluzione dell'esercizio 19.2 Sia $v=i\in\{1,\dots,n\}$, allora

$$V(C_n-i) = \{1,\dots,i-1\}\cup\{i+1,\dots,n\}$$

$$E(C_n-i) = \{\{1,2\},\dots,\{i-2,i-1\}\} \cup \{\{i+1,i+2\},\dots,\{n-1,n\},\{n,1\}\}$$

Ma allora la funzione $f:\{1,\dots,n-1\}\to \{1,\dots,i-1\}\cup\{i+1,\dots,n\}$ definita da

$$f(j)=\Big\langle \begin{array}{lcl} i+j &\text{se} & j\le n-i\\ j-(n-i) =j+i-n &\text{se} & j\ge n-i+1\\ \end{array}$$

è un isomorfismo. Chiaramente $f$ è bigettiva. Inoltre

$$\{f(j),f(j+1)\} = \left\{ \begin{array}{lcl} \{i+j,i+j+1\} &... ...n-i \\ \{j+i-n,j+i-n+1\} &\text{se} &j>n-i \end{array}\right.$$

da cui segue che $f$ mette in bigezione i lati dei due grafi, ossia è un isomorfismo.     

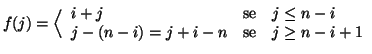
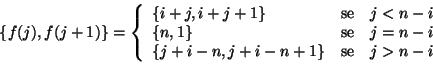
Soluzione dell'esercizio 19.3 Sia $G$ hamiltoniano, e sia $H$ un sottografo di $G$ isomorfo a $C_n$ che contiene tutti i vertici di $G$. Allora $H-v$ è un sottografo di $G-v$ che contiene tutti i vertici di $G-v$. Ma $H$ è isomorfo a un cammino (esercizio precedente) che è connesso. Si conclude allora invocando l'esercizio 16.3.     

Soluzione dell'esercizio 19.4 

    

Soluzione dell'esercizio 19.5 Usando l'esercizio precedente, possiamo supporre che $e=\{n,1\}$. Ma allora si verifica immediatamente che la funzione $f:\{1,\dots,n,n+1\}\to\{1,\dots,n\}\cup \{z\}$ definita da

$$f(i)=\big\langle \begin{array}{lcl} i & \text{se} & i\le n \\ z & \text{se} & i = n+1 \end{array}$$

è un isomorfismo tra $C_{n+1}$ e $C_n\%e$.     

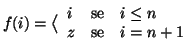
Soluzione dell'esercizio 19.6 Possiamo supporre che $e=\{n-,n\}$. Ma allora si verifica immediatamente che la funzione $f:\{1,\dots,n,n+1\}\to\{1,\dots,n\}\cup \{z\}$ definita da

$$f(i)=\big\langle \begin{array}{lcl} i & \text{se} & i\le n-1 \\ z & \text{se} & i = n\\ n & \text{se} & i = n+1 \end{array}$$

è un isomorfismo tra $P_{n+1}$ e $P_n\%e$.     

Soluzione dell'esercizio 19.7 

    

Soluzione dell'esercizio 19.8 

    

Soluzione dell'esercizio 19.9 

    

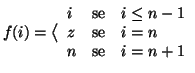
Soluzione dell'esercizio 19.10 

    

Soluzione dell'esercizio 19.11 

    

Soluzione dell'esercizio 19.12 

    

Soluzione dell'esercizio 19.13 

    

Soluzione dell'esercizio 20.1 

    

Soluzione dell'esercizio 20.3 Un cammino in $G$ che congiunge due vertici diversi da $v$ non può passare per $v$, in quanto i vertici di un cammino, eccetto al più il primo e l'ultimo, hanno grado almeno $2$.     

Soluzione dell'esercizio 20.4 Per l'esercizio precedente $T-v$ è connesso. D'altra parte se $T-v$ avesse un ciclo, questo sarebbe un ciclo anche in $T$.     

Soluzione dell'esercizio 20.5 Sia $G$ un grafo connesso con $n$ vertici, indichiamo con $f(G)$ il numero di foglie di $G$. Se $n=2$ allora il numero di foglie è esattamente $f=2$. Se $n\ge3$ proviamo che allora il numero di foglie è $f(G) \le n-1$. Lo proviamo per induzione su $n$. Se $n=3$ si vede facilmente, analizzando tutti i grafi connessi con $3$ vertici (sono solo 2) che il massimo numero di foglie è $2$ (uno ne ha $2$ e l'altro non ne ha). Supponiamo la tesi vera per $n$ e sia $G$ un grafo connesso con $n+1$ vertici. Se $G$ non ha foglie allora la tesi è vera ( $f(G)=0\le n$) altrimenti sia $v\in V(G)$ una foglia. Il grafo $G-v$ è connesso, ha $n$ vertici e quindi, per ipotesi di induzione, $f(G-v)\le n-1$. D'altra parte $G$ ha al più una foglia in più di $G-v$ (il vertice $v$) e quindi

$$f(G) \le f(G-e) + 1 \le n-1 +1 =n$$

che è la tesi.

Un esempio è dato dal grafo $G$ definito da:

$$V(G) = \{0,1,\dots,n-1\}$$

$$E(G) = \{\{0,i\}\mid i=1,\dots,n-1\}$$

Si può provare che a meno di isomorfismo questo è l'unico grafo connesso con $n$ vertici e $n-1$ foglie. Infatti sia $G$ un tale grafo. $G$ deve avere un vertice di grado $n-1$. Infatti se $k$ è il grado dell'unica non foglia, allora

$$\sum_{v\in\vee (G)}\deg(v)=n-1+k = 2 \left\vert E(G)\right\vert$$

d'altra parte se $G$ è connesso, $\left\vert E(G)\right\vert\ge n-1$ quindi $k\ge n-1$. È altresì chiaro che un vertice di un grafo con $n$ vertici può avere grado al più $n-1$ e quindi $k=n-1$.     

Soluzione dell'esercizio 20.6 Siano $T_1,\dots,T_k$ le componenti connesse di $F$, allora ogni $T_i$ è un albero, ma allora per ogni $i$ si ha $\left\vert(\right\vert V(T_i))=\left\vert(\right\vert E(T_i))+1$. Dal fatto che $\sum_{i=1}^k\left\vert(\right\vert V(T_i)=\left\vert(\right\vert V)$ e $\sum_{i=1}^k\left\vert(\right\vert E(T_i)=\left\vert(\right\vert E)$ segue immediatamente la tesi.     

Soluzione dell'esercizio 21.1 Siano $v,u\in V(G)=V(G')$, allora, dato che $G'$ è connesso, esiste una passeggiata $P=(v_0,\dots, v_k)$ in $G$ che congiunge $U$ a $v$ , ossia:

• $v_0=u$ e $v_k=v$
• per ogni $i$ si ha $\{v_i,v_{i+1}\}\in E(G')$.

Dato che $G'$ è un sottografo di $G$ si ha che $E(G')\subseteq E(G)$ e quindi $\{v_i,v_{i+1}\}\in E(G)$ per ogni $i$. Di conseguenza $P$ è una passeggiata in $G$ che congiunge $u$ a $v$. Per l'arbitrarietà di $u,v\in V(G)$ si ha la tesi.     

Soluzione dell'esercizio 21.2 

    

Soluzione dell'esercizio 21.3 Sia $T$ un albero di copertura di $G$. Chiaramente $\left\vert V(T)\right\vert=\left\vert V(G)\right\vert$ e dato che $T$ è un sottografo di $G$ allora $\left\vert E(T)\right\vert\le \left\vert E(G)\right\vert$ e quindi, usando la formula che lega il numero di lati con il numero dei vertici di un albero, si ha

$$\left\vert E(G)\right\vert\ge \left\vert E(T)\right\vert = \left\vert V(T)\right\vert - 1 = \left\vert V(G)\right\vert - 1.$$

    

Soluzione dell'esercizio 21.4 

    

Soluzione dell'esercizio 23.1