

Next: Lezione 18
Up: Matematica Discreta (II modulo)
Previous: Lezione 16
Subsections
Definizione 17.1
Sia
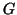
un grafo e sia
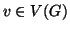
, chiameremo
grado di
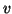
il numero
(cardinale)
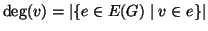
. Diremo che
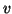
ha
grado finito se
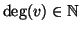
.
Dimostrazione.
Siano
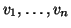 i vertici di
i vertici di 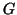 e
e
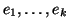 i suoi
lati. Per ogni
i suoi
lati. Per ogni
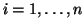 e
e
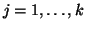 consideriamo il numero
consideriamo il numero
Dalle proprietà associativa e commutativa della somma si ha evidentemente che
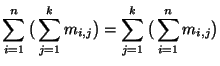 |
(10) |
Ma fissato 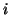 il numero
il numero
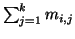 è uguale alla
cardinalità dell'insieme
è uguale alla
cardinalità dell'insieme
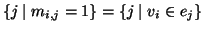 che è uguale al numero dei lati che contengono
che è uguale al numero dei lati che contengono 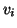 , ossia
, ossia
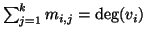 . Pertanto il lato sinistro dell'uguaglianza
(10) è pari a
. Pertanto il lato sinistro dell'uguaglianza
(10) è pari a
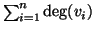 , ossia la somma dei gradi di
tutti i vertici.
, ossia la somma dei gradi di
tutti i vertici.
Invece, fissato 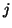 , il numero
, il numero
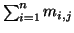 è pari alla
cardinalità dell'insieme
è pari alla
cardinalità dell'insieme
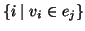 , che è uguale a
, che è uguale a 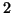 , dato
che ogni lato contiene esattamente due vertici. Ne consegue che il lato destro
della (10) è uguale a
, dato
che ogni lato contiene esattamente due vertici. Ne consegue che il lato destro
della (10) è uguale a
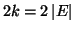 .
.

Proposizione 17.3
In un grafo il numero di vertici di grado dispari è pari.
Proposizione 17.4
Se

è un isomorfismo tra
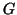
e
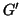
e
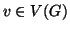
allora
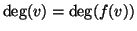
.
Definizione 17.5
Sia
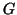
un grafo finito e sia
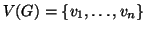
, si chiama
score
di
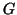
la successione (finita)
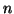
-pla dei gradi dei suoi vertici ovvero
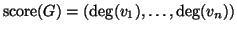
.
Per scrivere lo score abbiamo dovuto ordinare i vertici del grafo e, ordinamenti
diversi producono 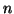 -ple diverse, ma che coincidono a meno di
riordinamento. Due score si considereranno quindi uguali se lo sono a meno di
riordinarli. Per comodità si ordineranno i vertici in modo che la successione
dei gradi sia non decrescente (i.e.
-ple diverse, ma che coincidono a meno di
riordinamento. Due score si considereranno quindi uguali se lo sono a meno di
riordinarli. Per comodità si ordineranno i vertici in modo che la successione
dei gradi sia non decrescente (i.e.
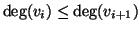 per ogni
per ogni 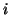 ).
).
Teorema 17.6
Se
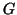
e
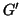
sono grafi isomorfi, allora
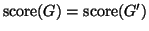
.
Osservazione 17.7
Non è vero il viceversa del precedente teorema, si vedano ad esempio i grafi
i due grafi di figura
6 dell'esercizio
14.11.


Next: Lezione 18
Up: Matematica Discreta (II modulo)
Previous: Lezione 16
Domenico Luminati
2004-03-18
![]() i vertici di
i vertici di ![]() e
e
![]() i suoi
lati. Per ogni
i suoi
lati. Per ogni
![]() e
e
![]() consideriamo il numero
consideriamo il numero
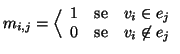
![]() , il numero
, il numero
![]() è pari alla
cardinalità dell'insieme
è pari alla
cardinalità dell'insieme
![]() , che è uguale a
, che è uguale a ![]() , dato
che ogni lato contiene esattamente due vertici. Ne consegue che il lato destro
della (10) è uguale a
, dato
che ogni lato contiene esattamente due vertici. Ne consegue che il lato destro
della (10) è uguale a
![]() .
.
![]()