L'insieme di tutte le permutazioni di X si denota con SX. Se
![]() e
e
![]() l'insieme delle permutazioni di
l'insieme delle permutazioni di
![]() si denota
semplicemente con Sn.
si denota
semplicemente con Sn.
L'insieme di tutte le permutazioni di X si denota con SX. Se
![]() e
e
![]() l'insieme delle permutazioni di
l'insieme delle permutazioni di
![]() si denota
semplicemente con Sn.
si denota
semplicemente con Sn.
Dim.
La composizione è associativa. Infatti per ogni ![]()
![]() .
.
L'applicazione identica
![]() è l'unità.
è l'unità.
Per definizione ogni ![]() è bigettiva e quindi esiste l'inversa
f-1 tale che
è bigettiva e quindi esiste l'inversa
f-1 tale che
![]() .
Chiaramente
.
Chiaramente
![]() .
.
![]()
Dim.
Un'applicazione
![]() è univocamente
determinata dalla k-upla
è univocamente
determinata dalla k-upla
![]() .
Ora f(1) può essere scelto
in n modi diversi, se si vuole che f sia iniettiva f(2) potrà essere
scelto tra tutti i numeri da 1 a n tranne f(1), quindi per f(2) si
hanno esattamente n-1 possibilità di scelta, analogamente per f(3) si
hanno n-2 scelte possibili e così vaia, supposto di aver scelto
.
Ora f(1) può essere scelto
in n modi diversi, se si vuole che f sia iniettiva f(2) potrà essere
scelto tra tutti i numeri da 1 a n tranne f(1), quindi per f(2) si
hanno esattamente n-1 possibilità di scelta, analogamente per f(3) si
hanno n-2 scelte possibili e così vaia, supposto di aver scelto
![]() ,
per f(i+1) si hanno n-i scelte possibili.Si
arriva in tal modo fino ad f(k) per il quale si hanno f(n-k+1) scelte. In
totale si ottengono quindi
,
per f(i+1) si hanno n-i scelte possibili.Si
arriva in tal modo fino ad f(k) per il quale si hanno f(n-k+1) scelte. In
totale si ottengono quindi
![]() applicazioni
iniettive diverse.
applicazioni
iniettive diverse.
![]()
Dim.
Segue dalla proposizione precedente applicata al caso n=k.
![]()
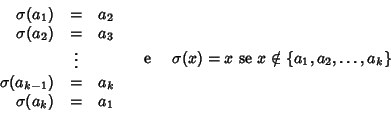
Dim.
Dal fatto che i due cicli sono disgiunti, si ha che l'insieme
![]() si spezza nell'unione di tre pezzi a due a due disgiunti:
si spezza nell'unione di tre pezzi a due a due disgiunti:
![]() essendo
essendo
![]()
![]() .
Ora se
.
Ora se ![]() si ha che
si ha che
![]() e quindi
e quindi
![]() e
e
![]() ,
in particolare
,
in particolare
![]() .
.
Se ![]() allora
allora
![]() e quindi
e quindi
![]() (si ricordi che
(si ricordi che ![]() lascia fissi
gli elementi non in B). E analogamente
lascia fissi
gli elementi non in B). E analogamente
![]() e quindi
e quindi
![]() .
Anche in questo caso si ha che
.
Anche in questo caso si ha che
![]() .
.
Completamente analoga è la verifica che se ![]() allora
allora
![]() .
In altre parole
.
In altre parole
![]() per ogni
per ogni
![]() ,
ossia
,
ossia
![]() .
.
![]()
Dim.
Segue immediatamente dal teorema e
dall'osservazione precedenti.
![]()