Lezione 10 (22 marzo 1999 h. 9.30-10.30)

Dimostrazione del Teorema di decomposizione in cicli disgiunti

Dim.  Se $\sigma(i)=i$ per ogni $i=\{1,\dots,n\}$ non c'è nulla da dimostrare. Sia i₁ il primo numero in $\{1,\dots,n\}$ tale che $\sigma(i_1)\ne i_1$. Scriviamo

$$i_1,\sigma(i_1),\sigma^2(i_1),\dots,\sigma^k(i_1),\sigma^{k+1}(i_1),\dots$$

dato che le espressioni $\sigma^k(i_1)$ sono infinite, ma i loro valori sono un numero finito, esistono almeno due diversi naturali, k<m tali che $\sigma^k(i_1)=\sigma^m(i_1)$ (i.e. l'applicazione $\mathbb N\to\{1,2,\dots,n\}$, $k\mapsto\sigma^k(i_1)$ non può essere iniettiva). Posto m=k+h, si ha che $\sigma^k(i_1)=\sigma^k(\sigma^h(i_1))$ e dato che $\sigma^k$ è bigettiva si ha che $i_1=\sigma^h(i_1)$. Sia h₁ il primo naturale positivo tale che $i_1=\sigma^{h_1}(i_1)$.

Si noti che gli elementi $i_1,\sigma(i_1),\dots,\sigma^{h_1-1}(i_1)$ sono tra loro distinti, infatti se così non fosse si contradirebbe la minimalità di h₁ (si ragioni come si è fatto per mostrare l'esistenza di h₁). Cosideriamo allora il ciclo $\pi_1=(i_1\ \sigma(i_1) \dots \sigma^{h_1-1}(i_1))$. Osserviamo che se $x\in\{i_1,\sigma(i_1),\dots,\sigma^{h_1-1}(i_1)\}$ allora $\sigma(x)=\pi_1(x)$.

Se $\sigma(x)=x$ per ogni $x\notin \{i_1,\sigma(i_1),\dots,\sigma^{h_1-1}(i_1)\}$ allora $\sigma(x)=\pi_1(x)$ per ogni x e quindi abbiamo finito, altrimenti sia i₂ il primo elemento per cui $\sigma(i_2)\ne i_2$ e $i_2 \notin \{i_1,\sigma(i_1),\dots,\sigma^{h_1-1}(i_1)\}$ e sia h₂ il minimo intero positivo per cui $i_2=\sigma^{h_2}(i_2)$ e sia $\pi_2=(i_2 \ \sigma(i_2) \dots \sigma^{h_2-1}(i_2))$.

Si osservi che $\{i_1,\sigma(i_1),\dots,\sigma^{h_1-1}(i_1)\}\cap\{i_2,\sigma(i_2),\dots,\sigma^{h_2-1}(i_2)\}=\varnothing$e che se $x\in\{i_1,\sigma(i_1), \dots, \sigma^{h_1-1}(i_1)\}\cup\{i_2,\sigma(i_2), \dots, \sigma^{h_2-1}(i_2)\}$allora $\sigma(x)=\pi_1\pi_2(x)$. Il procedimento si può evidentemente iterare costruendo ad ogni passo un ciclo che è disgiunto da tutti i precedenti e che agisce come $\sigma$ sul suo supporto.

Dato che stiamo lavorando sull'insieme finito $\{1,2,\dots, n\}$, tale procedimente deve terminare, producendo la decomposizione cercata.

L'unicità di tale decomposizione osservando che se $\sigma=\pi_1\dots\pi_k$con $\pi_i$ cicli a due a due disgiunti, allora i cicli determinati dal procedimento precedente sono proprio i $\pi_i$, eventualmente dati in ordine diverso.     $\square$

Osservazione 10.1   La dimostrazione della proposizione precedente fornisce un algoritmo per determinare in modo effettivo la decomposizione in cicli di una permutazione.

Segno di una permutazione

Definizione 10.2   Sia $\sigma\in S_n$, definiamo segno di $\sigma$ il numero

$$\varepsilon(\sigma)=(-1)^{\sum_{i=1}^s(l(\pi_i)-1)}$$ (10)

dove $\sigma=\pi_1\pi_2\dots\pi_s$ è la decomposizione in cicli disgiunti e $l(\pi_i)$ è la lunghezza del ciclo $\pi_i$.

Proposizione 10.3   Se $\sigma,\tau\in S_n$ allora

$$\varepsilon(\sigma_1\sigma_2)=\varepsilon(\sigma_1)\varepsilon(\sigma_2)$$ (11)

Dim.  Osserviamo innanzitutto che dalla definizione segue immediatamente che se $\tau$ è una trasposizione allora $\varepsilon(\tau)=-1$.

Supponiamo di sapere che la formula (11) valga quando $\sigma_2$ è una trasposizione, ossia che:

$$\varepsilon(\sigma\tau)=\varepsilon(\sigma)\varepsilon(\tau)... ...epsilon(\sigma) \quad \hbox{\rm {per ogni trasposizione }}\tau$$ (12)

Usando questo fatto, osserviamo allora che se $\sigma=\tau_1\tau_2\dots\tau_k$è una decomposizione come prodotto di trasposizioni, si ha

$$\varepsilon(\sigma)= \varepsilon(\tau_1\dots\tau_n)= -\varep... ...n-1})= (-1)^2\varepsilon(\tau_1\dots\tau_{n-2})= \dots= (-1)^k$$ (13)

Se ora $\sigma_2=\tau_1\dots\tau_k$ è una decomposizione in prodotto di trasposizioni, procedendo esattamente come sopra, si ha:

$$\varepsilon(\sigma_1\sigma_2)= \varepsilon(\sigma_1\tau_1\dot... ...ma_1\tau_1\dots\tau_{k-1})= \dots= (-1)^k\varepsilon(\sigma_1)$$

e quindi, usando la (13), $\varepsilon(\sigma_1\sigma_2)=\varepsilon(\sigma_1)\varepsilon(\sigma_2)$.

Resta da dimostrare la (12), che viene lasciata per esercizio (non facile).     $\square$

Esercizio 10.1    Si osservi che se $(a\ a_1 \dots a_k)$ e $(b\ b_1 \dots b_h)$ sono cicli disgiunti e $(a\ a_1 \dots a_k \ b \ \ b_1 \dots b_h)$ è un ciclo, allora risulta:

$$\begin{eqnarray*}(a\ a_1 \dots a_k \ b \ b_1 \dots b_h)(a\ b)&= &(a \ b_1 \dots... ... \dots b_h)(a\ b)&= &(a \ b_1 \ \dots b_h \ b \ a_1 \dots a_k) \end{eqnarray*}$$

Si usi questo fatto per provare la (12) nella dimostrazione della proposizione precedente.

Soluzione

Osservazione 10.4   La formula (13) mostra che data una permutazione, il numero di trasposizioni che costituiscono una sua decomposizione deve essere sempre pari o sempre dispari, a secondo che il segno della peremutazione sia 1 oppure -1. Una permutazione sarà detta pari se il suo segno è 1, sarà detta dispari se il suo segno è -1.

Sottogruppo generato

Proposizione 10.5   Sia G un gruppo, e siano $\{H_\lambda\}_{\lambda\in\Lambda}$ una famiglia di sottogruppi di G. Allora $\bigcap_{\lambda\in\Lambda}H_\lambda$ è un sottogruppo di G.

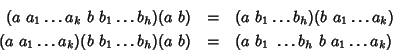
Dim.  Indichiamo con $H=\bigcap H_\lambda$. Se $h_1,h_2\in H$ allora per ogni $\lambda$ $h_1,h_2\in H_\lambda$ e poiché questi sono tutti sottogrupi, $h_1h_2\in H_\lambda$ per ogni $\lambda$ ovvero $h_1h_2\in H$. (È verificata la (1) della definizione di sottogruppo).

Ogni $H_\lambda$ è un sottogruppo, quindi $1\in H_\lambda$ per ogni $\lambda$ e pertanto $1\in H$ (È verificata la (2) della definizione di sottogruppo).

Sia $h\in H$ allora $h\in H_\lambda$ per ogni $\lambda$. Essendo gli $H_\lambda$ dei sottogruppi $h^{-1}\in H_\lambda$ per ogni $\lambda$ ovvero $h^{-1}\in H$ (È verificata la (3) della definizione di sottogruppo).     $\square$

Osservazione 10.6   I tre passi della dimostrazione precedente, presi uno alla volta, mostrano che la proposizione rimane vera se nell'enunciato si sostituiscono le parole gruppo e sottogruppo con semigruppo e sottosemigruppo oppure con monoide e sottomonoide

Definizione 10.7   Sia G un gruppo e sia $S\subseteq G$ denoteremo con $\left\langle {}S\right\rangle$ il più piccolo sottogruppo di G che contiene S. Ossia $\left\langle {}S\right\rangle$ è un sottogruppo con le seguenti due proprietà:

1.

  $S\subseteq\left\langle {}S\right\rangle$,

2.

  se H è un sottogruppo di G e $S\subseteq H$ allora $\left\langle {}S\right\rangle\subseteq H$.

$\left\langle {}S\right\rangle$ si chiama sottogruppo generato da S.

Proposizione 10.8   Se S è un sottinsieme di G, il sottogruppo generato da S esiste ed è unico. E risulta:

$$\left\langle {}S\right\rangle=\bigcap_{S\subseteq H\le G}H$$

ossia $\left\langle {}S\right\rangle$ è l'intersezione di tutti i sottogruppi di G che contengono S.

Dim.  Osserviamo che $\bigcap_{S\subseteq H\le G}H$ è un sottogruppo (per la proposizione 10.5) e d'altra parte se $S\subseteq H_0\le G$ allora $\bigcap_{S\subseteq H\le G} H\subseteq H_0$, ossia $\bigcap_{S\subseteq H\le G}H$ verifica le 1 e 2 della definizione di sottogruppo generato.

Che il sottogruppo generato sia unico segue dal fatto che se H₁ e H₂verificano le 1 e 2 della definizione di sottogruppo generato allora necessariamente $H_1\subseteq H_2$ (H₁ è minimo e H₂ è un sottogruppo che contiene S) e, scambiando i ruoli di H₁ e H₂, anche $H_2\subseteq H_1$.     $\square$

Osservazione 10.9   La definizione di sottogruppo generato si generalizza immediatamente al caso di monoidi e semigruppi, e la sua esistenza ed unicità si dimostra esattamente nello stesso modo.

Osservazione 10.10   Sia T l'insieme delle trasposizioni di S_n. Il corollario 9.10 ci dice allora che $\left\langle {}T\right\rangle=S_n$.