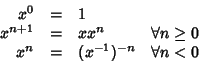Next: Lezione 9 (18 marzo
Up: Matematica Discreta
Previous: Lezione 7 (15 marzo
Subsections
Definizione 8.1
Sia
X un insieme. Un'
operazione binaria su
X è un'applicazione
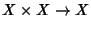
.
Se
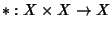
è un'operazione si scriverà
x1*
x2 piuttosto che
*(
x1,
x2).
Un'operazione * si dice
associativa se
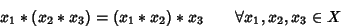 |
(2) |
Una coppia (
X,*) dove
X è un insieme e * è un'operazione
associativa su
X si dice un
semigruppo.
Di norma, se non ci saranno ambiguità, l'operazione di un semigruppo viene
denotata con 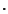 (notazione moltiplicativa) o con + (notazione
additiva). Nel primo caso il punto viene quasi sempre omesso.
(notazione moltiplicativa) o con + (notazione
additiva). Nel primo caso il punto viene quasi sempre omesso.
Definizione 8.2
Sia (
X,*) un monoide, un elemento
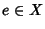
si dice una
unità
sinistra se
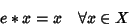 |
(3) |
un elemento
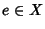
si dice una
unità destra se
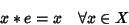 |
(4) |
un elemento che sia contemporaneamente una unità sinistra e destra si dice
una
unità.
Un semigruppo si dice un monoide se possiede una unità.
Proposizione 8.3
Sia (
X,*) un semigruppo e siano
e una unità sinistra e
e' una
unità destra, allora
e=
e'.
Dim.
Si ha e'=e*e'=e, dove la prima uguaglianza vale poiché e è una unità
sinistra e la seconda in quanto e' è una unità destra.

Osservazione 8.4
In particolare dalla
proposizione precedente segue che in un monoide l'unità è unica.
L'unità di un monoide viene usualmente denotata con 1 se si sta usando
la notazione moltiplicativa o con 0 se si sta usando la notazione
additiva.
Definizione 8.5
Sia
X un monoide, e sia
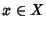
,
un elemento
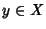
si dice un
inverso sinistro di
x se
yx=1, si dice un inverso destro se
xy=1 si
dice un inverso se è inverso sia destro che sinistro.
Un monoide in cui ogni elemento possiede un inverso si chiama un
gruppo
Proposizione 8.6
Sia
X un monoide,
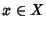
e siano
y e
y' rispettivamente un inverso
destro ed un inverso sinistro di
x, Allora
y=
y'.
Dim.
y=y1=y(xy')=(yx)y'=1y'=y'.

Osservazione 8.7
In particolare la
proposizione precedente garantisce che in un gruppo ogni elemento ha un unico
inverso.
L'inverso di un elemento
x viene denotato con
x-1 con la notazione
moltiplicativa e con -
x con la notazione additiva.
Definizione 8.8
Una operazione sull'insieme
X si dice
commutativa se per ogni
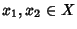
si ha
x1x2=
x2x1. Se l'operazione di un semigruppo
[risp. monoide, gruppo] è commutativa, il semigruppo [risp. monoide,
gruppo] sarà detto commutativo.
Esercizio 8.1
Siano
X,
Y insiemi e sia * un'operazione su
Y. Su
YX si definisca
l'operazione,

ponendo
Si provi che
- 1.
- se (Y,*) è un semigruppo, anche
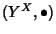 lo
è;
lo
è;
- 2.
- se (Y,*) è un monoide, anche
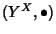 lo è;
lo è;
- 3.
- se (Y,*) è un gruppo, anche
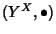 lo è;
lo è;
- 4.
- se * è commutativa, allora anche
 lo è.
lo è.
Soluzione
Esercizio 8.2
Si dimostri che se
G è un gruppo allora per ogni
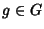
si ha che
(
g-1)
-1=
g.
Soluzione
Esercizio 8.3
Sia
G un gruppo e siano
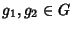
si provi che
(
g1g2)
-1=
g2-1g1-1.
Si dimostri che
(
g1g2)
-1=
g1-1g2-1 per ogni
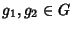
se
e solo se il gruppo è commutativo.
Soluzione
Esercizio 8.4
Sia
M un monoide e sia
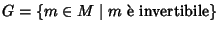
.
Si
dimostri che
G con l'operazione del monoide è un gruppo.
Soluzione
Definizione 8.9
Sia
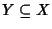
.
Se
X è un semigruppo, diremo che
Y è un
sottosemigruppo di
X se
- 1.
-
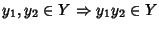
Se
X è un monoide diremo che
Y è un
sottomonoide di
X se è
un sottosemigruppo ed in più
- 1.
-
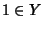
Se
X è un gruppo, diremo che
Y è un
sottogruppo di
X se è
un sottomonoide ed in più
- 1.
-
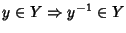
Per indicare che
Y è un sottogruppo di
X si scriverà anche
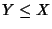
.
Proposizione 8.10 (criterio del sottogruppo)
Sia
G un gruppo e sia
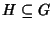
,
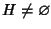
.
H è un
sottogruppo se e solo se
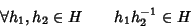 |
(5) |
Dim.
Se H è un sottogruppo, e
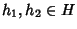 ,
allora per la 3
della definizione di sottogruppo si ha che
,
allora per la 3
della definizione di sottogruppo si ha che
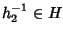 e quindi per la 1
e quindi per la 1
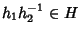 .
.
Viceversa, supponiamo che valga la (5). Dato che
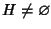 esiste
esiste 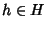 ,
ma allora per (5) si ha che
,
ma allora per (5) si ha che
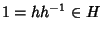 e
quindi vale la 2 di 8.9. Dato
e
quindi vale la 2 di 8.9. Dato 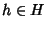 ,
visto che
,
visto che 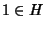 si ha allora che
si ha allora che
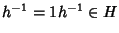 ossia vale anche la 3 di
8.9. Infine, se
ossia vale anche la 3 di
8.9. Infine, se
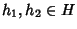 ,
allora
,
allora
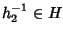 e quindi
e quindi
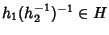 .
D'altra parte, per l'esercizio 8.2,
(h2-1)-1=h2 e quindi
.
D'altra parte, per l'esercizio 8.2,
(h2-1)-1=h2 e quindi
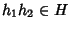 ,
ovvero vale la 1 di
8.9.
,
ovvero vale la 1 di
8.9.

Esercizio 8.5
Si provi che i sottogruppi di
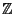
sono tutti e soli gli insiemi della forma
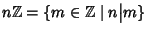
.
Soluzione
Esercizio 8.6
Sia
X un gruppo, per ogni
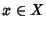
e
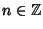
si definisce
xn ponendo
Si provi che per ogni
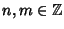
e per ogni
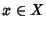
si ha
| x-n |
= |
(x-1)n |
(6) |
| xnxm |
= |
xn+m |
(7) |
| (xn)-1 |
= |
x-n |
(8) |
| (xn)m |
= |
xnm |
(9) |
Soluzione



Next: Lezione 9 (18 marzo
Up: Matematica Discreta
Previous: Lezione 7 (15 marzo
Domenico Luminati
1999-07-08
![]() (notazione moltiplicativa) o con + (notazione
additiva). Nel primo caso il punto viene quasi sempre omesso.
(notazione moltiplicativa) o con + (notazione
additiva). Nel primo caso il punto viene quasi sempre omesso.
![]()
![]()
![]() ,
allora per la 3
della definizione di sottogruppo si ha che
,
allora per la 3
della definizione di sottogruppo si ha che
![]() e quindi per la 1
e quindi per la 1
![]() .
.
![]() esiste
esiste ![]() ,
ma allora per (5) si ha che
,
ma allora per (5) si ha che
![]() e
quindi vale la 2 di 8.9. Dato
e
quindi vale la 2 di 8.9. Dato ![]() ,
visto che
,
visto che ![]() si ha allora che
si ha allora che
![]() ossia vale anche la 3 di
8.9. Infine, se
ossia vale anche la 3 di
8.9. Infine, se
![]() ,
allora
,
allora
![]() e quindi
e quindi
![]() .
D'altra parte, per l'esercizio 8.2,
(h2-1)-1=h2 e quindi
.
D'altra parte, per l'esercizio 8.2,
(h2-1)-1=h2 e quindi
![]() ,
ovvero vale la 1 di
8.9.
,
ovvero vale la 1 di
8.9.
![]()