


Next: Lezione 22 (29 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 20 (22 maggio
Subsections
Sia (T,r) un albero radicato, sull'insieme dei vertici sono allora definite le
due relazioni 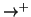 e
e 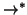 ,
ovvero la chiusura transitive e la
chiusura transitiva e riflessiva della relazione
,
ovvero la chiusura transitive e la
chiusura transitiva e riflessiva della relazione 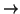 di
paternità.
di
paternità.
Ricordiamo la seguente
Definizione 21.1
Un
ordinamento parziale su un insieme
X è una relazione
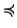
che sia
- 1.
- riflessiva (i. e.
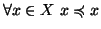 )
)
- 2.
- antisimmetrica (i.e.
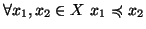 e
e
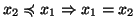 )
)
- 3.
- transitiva (i.e.
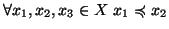 e
e
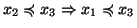 )
)
un ordinamento partziale
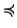
su
X si dice un
ordinamento
totale se in più
- 4
- per ogni
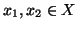
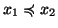 oppure
oppure
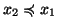 .
.
Proposizione 21.2
La relazione
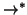
è un ordinamento parziale. E la relazione
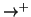
è
l'ordinamento stretto associato a
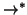
ossia
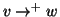
se e solo se
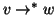
e
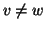
.
Dimostrazione.

Definizione 21.3
Sia
X un insieme e sia
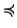
un ordinamento parziale su
X. Diremo
che
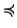
è
ben fondato se ogni successione discendente ha
minimo, ossia se per ogni
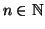
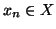
sono tali che
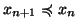
allora esiste un
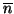
tale che
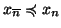
per ogni
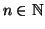
(in particolare se
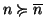
allora
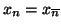
)).
Lemma 21.4
In un albero radicato l'insieme dei predecessori di un vertice è
finito. Formalmente, se (
T,
r) è un albero radicato, allora per ogni
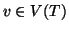
si ha che l'insieme
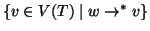
è finito.
Dimostrazione.

Teorema 21.5
L'ordinamento
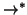
è ben fondato.
Dimostrazione.

Teorema 21.6 (Induzione sugli alberi)
Sia (
T,
r) un albero radicato e per ogni
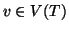
sia
P(
v) una
proposizione. Si supponga che:
- 1.
- P(r) sia vera;
- 2.
- per ogni
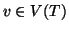 si ha che
si ha che
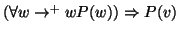 .
Allora P(v) è vera per ogni
.
Allora P(v) è vera per ogni 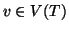 .
.
Dimostrazione.

Osservazione 21.7
Si osservi che nella dimostrazione del teorema precedente non si è mai usato
il fatto che si stesse parlando di alberi radicati, ma soltanto che
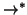
fosse un ordinamento ben fondato sull'insieme dei vertici, e che tale insieme
possedesse un minimo rispetto a tale ordinamento. La stessa dimostrazione
può quindi essere usata per dimostrare il seguente teorema
Teorema 21.8 (Induzione ben fondata)
Sia
X un insieme e sia
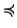
un ordinamento ben fondato su
X cha
ammette minimo
x0 (i.e.esiste
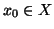
tale che
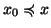
per
ogni
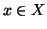
). Per ogni
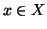
sia
P(
x) una proposizione. Si supponga
che:
- 1.
- P(x0) sia vera;
- 2.
- per ogni
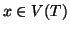 si ha che
si ha che
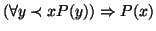 (dove
(dove 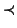 è una abbreviazione per
è una abbreviazione per
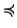 e
e 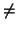 ).
).
Allora
P(
x) è vera per ogni
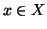
.



Next: Lezione 22 (29 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 20 (22 maggio
Domenico Luminati
2000-06-14
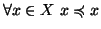 )
)
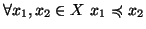 e
e
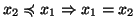 )
)
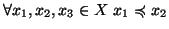 e
e
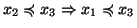 )
)
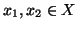
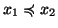 oppure
oppure
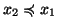 .
.
![]()
![]()
![]()
![]()