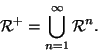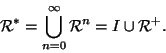Next: Lezione 21 (23 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 19 (16 maggio
Subsections
Alberi radicati
Definizione 20.1
Un
albero con radice è una coppia (
T,
r) con
T un albero e
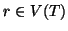
un vertice fissato che sarà detto
radice.
Se (
T,
r) e (
T',
r') sono due alberi radicati, si dirà che sono isomorfi
(come alberi radicati) se esiste un isomorfismo di grafi
f tra
T e
T' tale che
f(
r)=
r', e si scriverà
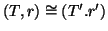
.
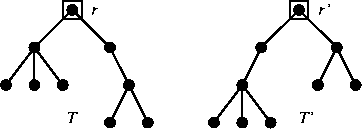
Esercizio 20.1
Si considerino i grafi in figura
9. Si provi che
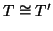
ma
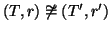
.
Figure 9:
Gli alberi radicati dell'esercizio 20.1
 |
Soluzione
La relazione  di ``paternità'' in un albero radicato
di ``paternità'' in un albero radicato
Dato un albero radicato, (T,r) per ogni vertice 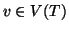 indichiamo con
Pv l'unico cammino che congiunge r con v.
indichiamo con
Pv l'unico cammino che congiunge r con v.
Proposizione 20.2
Sia (
T,
r) un albero radicato e sia
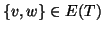
,
allora vale una e una
sola delle seguenti:
- 1.
- v è un vertice di Pw
- 2.
- w è un vertice di Pv.
Dimostrazione.
Proviamo che ne vale almeno una. Se non vale la (1), allora
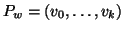 con v0=r, vk=w e
con v0=r, vk=w e 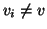 per ogni i. Ma allora,
dato che
per ogni i. Ma allora,
dato che
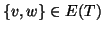 ,
,
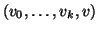 è un cammino che congiunge r
a v, per l'unicità di tale cammino
è un cammino che congiunge r
a v, per l'unicità di tale cammino
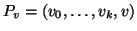 ,
e quindi vale la (2).
,
e quindi vale la (2).
Proviamo ora che non possono valere contemporaneamente. Se vale la (1), allora
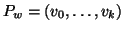 con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
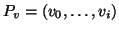 .
Dato che,
.
Dato che,
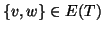 ,
,
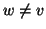 ,
quindi
i<k, e dato che Pw è un cammino
,
quindi
i<k, e dato che Pw è un cammino
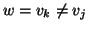 per ogni j<k, quindi w
non compare in
per ogni j<k, quindi w
non compare in
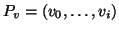 .
.

Definizione 20.3
Sia (
T,
r) un albero radicato, e siano
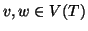
,
diremo che
v è
padre di
w, o che
w è figlio di
v, e lo indicheremo con
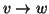
,
se
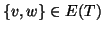
e
v è un vertice di
Pw.
Proposizione 20.4
Sia (
T,
r) un albero radicato, e sia
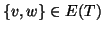
allora o
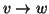
o
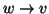
.
Inoltre per ogni
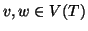
,
se
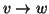
allora
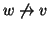
.
Dimostrazione.
È semplicemente la proposizione precedente tradotta in termini della relazione
 .
.

Cenni sui grafi diretti
Definizione 20.5
Un
grafo diretto è una coppia (
V,
E) dove
V è un insieme e
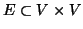
.
Gli elementi di
E vengono ancora chiamati lati e dati
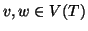
scriveremo
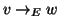
,
o più semplicemente
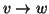
per dire
che
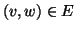
.
Osservazione 20.6
Intuitivamente un grafo diretto può essere pensato come un grafo, in cui
sono specificati dei ``versi di percorrenza'' degli archi che congiungono due
punti. Un po' come la mappa di una città in cui si tenga conto dei sensi
unici.
Si osservi che, a differenza dei grafi dove tra due vertici cè
soltanto un lato e non ci sono lati che vanno da un vertice a se stesso, tra
due vertici v e w di un grafo diretto ci possono essere entrambi i lati
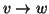 e
e 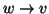 ,
e si possono avere anche lati del tipo
,
e si possono avere anche lati del tipo 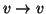 (vedi
figura 10).
(vedi
figura 10).
Figure 10:
Un grafo diretto
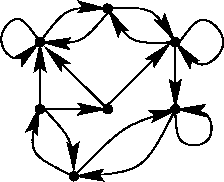 |
Si noti però che l'osservazione
14.2 mostra che dare un grafo è
equivalente a dare un grafo diretto simmetrico (i.e. se
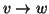
anche
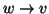
)
e antiriflessivo (i.e.
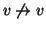
per ogni
v).
Osservazione 20.7
La proposizione
20.4 può essere interpretata dicendo che ogni
albero radicato può essere dotato in modo naturale di una struttura di grafo
diretto, in modo che ad ogni lato dell'albero corrisponda uno ed un solo lato
del grafo diretto.
Esercizio 20.2
Si diano le definizioni di passeggiata diretta, cammino diretto, ciclo diretto
in un grafo diretto e si provi che due vertici sono congiungibili da una
passeggiata diretta se e solo se sono congiungibili da un cammino diretto. Si
usi questo fatto per provare che la relazione ``essere congiungibili da un
cammino diretto'' è una relazione transitiva e riflessiva sull'insieme dei
vertici di un grafo diretto. È vero che è una relazione d'equivalenza?
Soluzione
Ricordiamo la definizione di relazione tra insiemi:
Definizione 20.8
Se
X e
Y sono insiemi, una
relazione tra X e
Y è un
sottinsieme
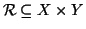
,
si usa la notazione
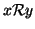
per dire
che
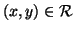
.
Definizione 20.9
Siano
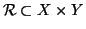
e
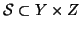
si definisce la
composizione di
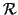
con
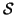
la relazione
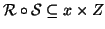
definita da
Esercizio 20.3
Si provi che se
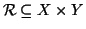
,
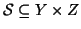
e
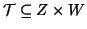
allora
Soluzione
Definizione 20.10
Dato un insieme
X si indica con
IX la relazione
identica su
X,
ovvero
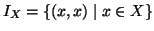
.
Esercizio 20.4
Si provi che se
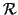
è una relazione tra
X e
Y, allora si ha che
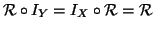
.
Soluzione
Esercizio 20.5
Siano
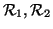
delle relazioni tra
X e
Y e sia
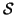
una relazione
tra
Y e
Z. Si provi che
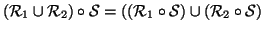
.
Soluzione
Definizione 20.11
Data una relazione
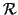
su un insieme
X, per ogni
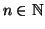
,
indicheremo
con
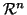
la relazione su
X definita ricorsivamente da:
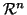
è detta la potenza
n-esima di
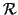
.
Definizione 20.12
Sia
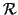
una relazione su
X, diremo che una relazione
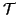
è una
chiusura transitiva di
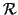
se
- 1.
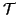 è transitiva
è transitiva
- 2.
-
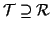
- 3.
- per ogni relazione transitiva su X che estende
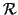 si ha
si ha
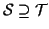 .
.
Teorema 20.13
Sia
X un insieme e
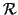
una relazione su
X, allora esiste una unica
chiusura transitiva di
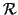
,
che è data da:
Definizione 20.14
Sia
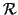
una relazione su
X, diremo che una relazione
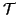
è una
chiusura transitiva e riflessiva di
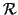
se
- 1.
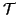 è transitiva e riflessiva
è transitiva e riflessiva
- 2.
-
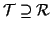
- 3.
- per ogni relazione transitiva e riflessiva su X che estende
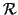 si ha
si ha
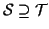 .
.
Teorema 20.15
Sia
X un insieme e
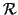
una relazione su
X, allora esiste una unica
chiusura transitiva e riflessiva di
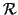
,
che è data da:
Osservazione 20.16
I due teoremi precedenti (
20.13 e
20.15) permettono
di sostituiore l'articolo indeterminativo nelle definizioni
20.12
e
20.14 con l'articolo determinativo. Si parlerà quindi
del
la chiusura transitiva e del
la chiusura transitiva e
riflessiva di una relazione
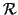
,
che saranno denotate rispettivamente con
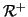
e
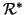
.
I teoremi già citati danno anche un modo costruttivo per
trovare
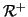
e
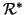
.
Esercizio 20.6
Sia
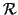
una relazione su
X e sia
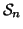
la successione di relazioni
definite ricorsivamente da:
Si provi che
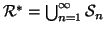
.
Soluzione
Esercizio 20.7
Si provi che
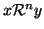
se e solo se esistono
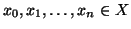
tali
che
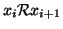
per ogni
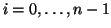
e
x0=
x,
xn=
y.
Soluzione
Esercizio 20.8
Si provi che se
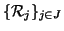
è un insieme di relazioni transitive su
X allora
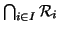
è ancora una relazione transitiva su
X.
Si usi questo fatto per mostrare che
essendo
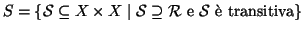
.
Soluzione
Esercizio 20.9
Si provi che se
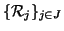
è un insieme di relazioni riflessive su
X allora
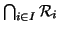
è ancora una relazione riflessiva su
X.
Si usi questo fatto per mostrare che
essendo
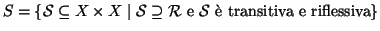
.
Soluzione



Next: Lezione 21 (23 maggio
Up: Matematica Discreta (II modulo)
Previous: Lezione 19 (16 maggio
Domenico Luminati
2000-06-14
![]() indichiamo con
Pv l'unico cammino che congiunge r con v.
indichiamo con
Pv l'unico cammino che congiunge r con v.
![]() con v0=r, vk=w e
con v0=r, vk=w e ![]() per ogni i. Ma allora,
dato che
per ogni i. Ma allora,
dato che
![]() ,
,
![]() è un cammino che congiunge r
a v, per l'unicità di tale cammino
è un cammino che congiunge r
a v, per l'unicità di tale cammino
![]() ,
e quindi vale la (2).
,
e quindi vale la (2).
![]() con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
con v0=r, vk=w ed esiste un i tale che vi=v. Ma
allora
![]() .
Dato che,
.
Dato che,
![]() ,
,
![]() ,
quindi
i<k, e dato che Pw è un cammino
,
quindi
i<k, e dato che Pw è un cammino
![]() per ogni j<k, quindi w
non compare in
per ogni j<k, quindi w
non compare in
![]() .
.
![]()
![]() .
.
![]()
![]() e
e ![]() ,
e si possono avere anche lati del tipo
,
e si possono avere anche lati del tipo ![]() (vedi
figura 10).
(vedi
figura 10).