


Next: Lezione 6 (14 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 4 (7 marzo
Subsections
Scrittura in base arbitraria dei naturali.
Dimostrazione.
Dimostriamo l'esistenza per induzione su n. Se n=0 basta prendere
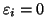 per ogni
per ogni
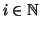 .
Supponiamo ora n>0 e che la tesi sia
vera per ogni k<n. Siano q,r tali che n=bq+r con
.
Supponiamo ora n>0 e che la tesi sia
vera per ogni k<n. Siano q,r tali che n=bq+r con 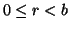 .
Dato che
.
Dato che 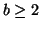 si ha che
si ha che
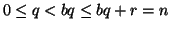 e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
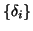 ,
costituita di interi tali che
,
costituita di interi tali che
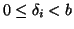 per
ogni i e tale che
per
ogni i e tale che
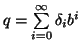 .
Ma
allora
.
Ma
allora
dove si è posto
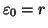 e
e
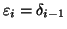 per ogni i>0. La
successione
per ogni i>0. La
successione
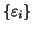 è definitivamente nulla, dato che lo è
è definitivamente nulla, dato che lo è
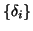 ed inoltre
ed inoltre
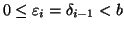 per ogni i>0 e
per ogni i>0 e
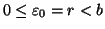 .
.
Dimostriamo ora l'unicità. Procediamo per induzione su n. Se
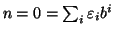 allora ogni addendo della somma essendo
nonnegativo, deve essere nullo e quindi
allora ogni addendo della somma essendo
nonnegativo, deve essere nullo e quindi
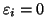 per ogni i.
per ogni i.
Supponiamo ora n>0 e che l'espressione in base b sia unica per
tutti i numeri k<n. Sia n tale che
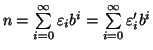 .
Allora possiamo scrivere
.
Allora possiamo scrivere
ma per l'unicità della divisione euclidea si ha che
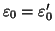 e
e
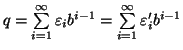 .
Come prima q<n e quindi per ipotesi di induzione si ha anche che
.
Come prima q<n e quindi per ipotesi di induzione si ha anche che
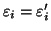 per ogni
per ogni 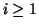 .
.

Definizione 5.2
Dati due interi
n,
m si dice che
n è un
divisore di
m (o che
m è un
multiplo di
n) se esiste un
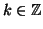
tale
che
m=
nk. Si indica con
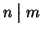
(si legge
n divide
m).
Esempio 5.3
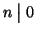
per ogni
n mentre se
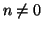
allora
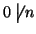
,
si ha
inoltre che
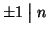
e
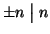
per ogni
n.
Dimostrazione.
1. Se m=kn e q=hm allora
q=hkm=(hk)m ossia
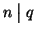 .
.
2. Se n=mk e m=nh allora m=hkm e quindi
m(1-hk)=0 e quindi o m=0 e quindi anche n=0, oppure 1-hk=0 ma
allora o h=k=1 e quindi n=m oppure n=m=-1 e quindi n=-m.

Definizione 5.5
Il numero
n si dice
primo se i suoi unici divisori sono
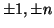
.
Definizione 5.6
Dati due interi
n,
m non entrambi nulli, si dice che
d è
un massimo comun divisoretra
n e
m se:
- 1.
-
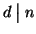 e
e
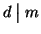 ;
;
- 2.
- Se
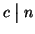 e
e
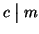 allora
allora
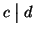 .
.
Proposizione 5.7
Se
d e
d' sono due massimi comun divisori tra
n e
m allora
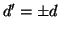
.
Dimostrazione.
d è un divisore comune di n e m, quindi poiché d'è un massimo comun divisore si ha che
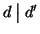 .
Scambiando i
ruoli di d e d' si ha allora che anche
.
Scambiando i
ruoli di d e d' si ha allora che anche
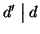 e quindi per
5.4 si ha che
e quindi per
5.4 si ha che 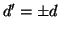 .
.

Definizione 5.8
Diremo che d è il massimo comun divisore di n e m se
è un massimo comun divisore positivo. La proposizione precedente
garantisce che se esiste il massimo comun divisore è unico. Esso
verrà indicato con (n,m).
Teorema 5.9
Dati due numeri
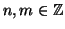
non entrambi nulli esiste il massimo
comun divisore di
n ed
m.
Dimostrazione.
Si consideri l'insieme
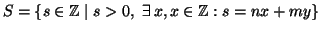 .
.
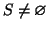 dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
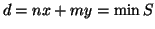 ,
dimostriamo che dè il massimo comun divisore. Se
,
dimostriamo che dè il massimo comun divisore. Se
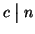 e
e
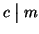 allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
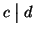 .
Dimostriamo ora che
.
Dimostriamo ora che
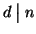 .
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con
.
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con 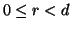 ,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e
,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e 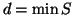 .
Quindi r=0 ossia
.
Quindi r=0 ossia
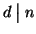 .
In modo analogo si prova che
.
In modo analogo si prova che
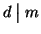 .
.

Osservazione 5.10
Dalla dimostrazione precedente segue che dati
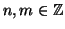
esistono
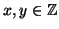
tali che
(
n,
m)=
nx+
my e che gli interi della forma
nx+
my con
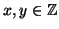
sono tutti e soli i multipli di (
n,
m).
Definizione 5.11
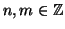
non entrambi nulli si dicono
coprimi se (
n,
m)=1.
Osservazione 5.12
(
n,
m)=1 se e solo se esistono
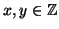
tali che
nx+
my=1. Ad
esempio (
n,
n+1)=1 per ogni
n. Infatti
1=(
n+1)1+
n(-1).
Proposizione 5.13
Sia
d=(
n,
m), allora
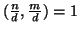
.
Dimostrazione.
d=nx+my e quindi
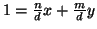 .
.

Il coefficiente binomiale
Definizione 5.14
Siano
n,
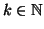
con
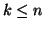
si pone
k-sottinsiemi
Definizione 5.15
Sia
X un insieme e
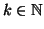
,
un sottinsieme
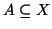
sarà detto un
k-sottinsieme se
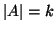
.
Denoteremo con
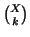
l'insieme dei
k-sottinsiemi di
X. I
k-sottinsiemi sono anche chiamati
k-combinazioni semplici.
Dimostrazione.

Definizione 5.17
Una k-combinazione con ripetizione di un insieme X è la scelta di
k elementi di X, che possono essere anche ripetuti, indipendentemente
dall'ordine.
Esempio 5.18
In altri termini una
k combinazione di
X è il risultato di
k scelte
indipendenti di elementi di
X.
Se
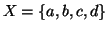
le seguenti sono delle 3-combinazioni:
aaa,
abb,
abc.
Si osservi che
aab e
aba danno la stessa combinazione, dato che non ci
interessa l'ordine in cui viene effettuata la scelta, ma soltanto il risultato
complessivo.
Esercizio 5.2
Si elenchino tutte le 3 combinazioni dell'insieme
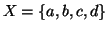
.
Soluzione
Proposizione 5.19
Se
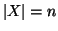
allora il numero di
k-combinazioni con ripetizione di
X è
dato da:
Il binomio di Newton
Proposizione 5.20
Siano
a,
b numeri reali, allora
Dimostrazione.

Una sestina al Superenalotto, è un sottinsieme di 6 elementi dell'insieme
dei numeri naturali da 1 a 90, quindi, per la proposizione 5.16
il numero di sestine possibili è dato da:
Pertanto, la probabilità di vincere giocando una sestina è pari a
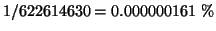 di vincere giocando una sestina. Se quindi il
gioco fosse equo, la puntata su una giocata dovrebbe essere pagata 622614630volte la posta. Dato che la puntata su una sestina costa 800 L., mi
aspetterei, in caso di successo, un premio di
di vincere giocando una sestina. Se quindi il
gioco fosse equo, la puntata su una giocata dovrebbe essere pagata 622614630volte la posta. Dato che la puntata su una sestina costa 800 L., mi
aspetterei, in caso di successo, un premio di
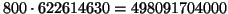 L.
L.
Un montepremi così alto non si è ancora visto!



Next: Lezione 6 (14 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 4 (7 marzo
Domenico Luminati
2000-06-14
![]() per ogni
per ogni
![]() .
Supponiamo ora n>0 e che la tesi sia
vera per ogni k<n. Siano q,r tali che n=bq+r con
.
Supponiamo ora n>0 e che la tesi sia
vera per ogni k<n. Siano q,r tali che n=bq+r con ![]() .
Dato che
.
Dato che ![]() si ha che
si ha che
![]() e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
![]() ,
costituita di interi tali che
,
costituita di interi tali che
![]() per
ogni i e tale che
per
ogni i e tale che
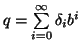 .
Ma
allora
.
Ma
allora
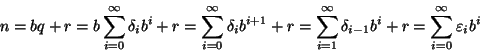
![]() allora ogni addendo della somma essendo
nonnegativo, deve essere nullo e quindi
allora ogni addendo della somma essendo
nonnegativo, deve essere nullo e quindi
![]() per ogni i.
per ogni i.
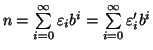 .
Allora possiamo scrivere
.
Allora possiamo scrivere
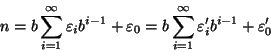
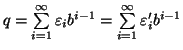 .
Come prima q<n e quindi per ipotesi di induzione si ha anche che
.
Come prima q<n e quindi per ipotesi di induzione si ha anche che
![]() .
.
![]()
![]() .
Scambiando i
ruoli di d e d' si ha allora che anche
.
Scambiando i
ruoli di d e d' si ha allora che anche
![]() e quindi per
5.4 si ha che
e quindi per
5.4 si ha che ![]() .
.
![]()
![]() .
.
![]() dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
dato che nn+mm>0 (dato che n e mnon sono entrambi nulli). Sia
![]() ,
dimostriamo che dè il massimo comun divisore. Se
,
dimostriamo che dè il massimo comun divisore. Se
![]() e
e
![]() allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
allora
n=ck e m=ch, quindi
d=nx+my=ckx+chy=c(kx+hy) ossia
![]() .
Dimostriamo ora che
.
Dimostriamo ora che
![]() .
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con
.
Consideriamo la divisione
euclidea tra n e d ossia n=dq+r con ![]() ,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e
,
se r>0 allora
r=n-dq=n-(nx+my)q=n(1-qx)+(-m)y è un elemento di S. Ciò è
assurdo perché r<d e ![]() .
Quindi r=0 ossia
.
Quindi r=0 ossia
![]() .
In modo analogo si prova che
.
In modo analogo si prova che
![]() .
.
![]()
![]() .
.
![]()
![]()
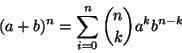
![]()