Ricordiamo gli assiomi (dovuti a Peano) che descrivono la struttura dei numeri naturali.
Dimostrazione.
Avendo l'esistenza, l'unicità segue immediatamente dall'iniettività di
![]() .
.
Supponiamo per assurdo che esista un ![]() tale che
tale che
![]() per
ogni n, allora sia
per
ogni n, allora sia
![]() .
Chiaramente
.
Chiaramente ![]() ,
in quanto
,
in quanto ![]() .
Se
.
Se ![]() ,
allora
,
allora
![]() e quindi
e quindi
![]() .
Ma allora
.
Ma allora
![]() ,
e questa è una contraddizione.
,
e questa è una contraddizione.
![]()
A partire dagli assiomi si possono definire ricorsivamente la somma, il prodotto di numeri naturali e il loro ordinamento.
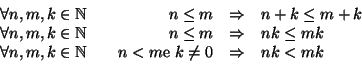
Dimostrazione.
Sia
![]() ,
allora
,
allora ![]() e se
e se ![]() anche
anche
![]() ,
quindi per l'assioma di induzione
,
quindi per l'assioma di induzione
![]() .
.
![]()
Dimostrazione.
Supponiamo che l'insieme
![]() non abbia minimo e proviamo che
allora
non abbia minimo e proviamo che
allora
![]() .
Chiamiamo B il suo complementare
(
.
Chiamiamo B il suo complementare
(
![]() )
e dimostriamo per induzione che
)
e dimostriamo per induzione che
Supponiamo che
![]() ,
allora
,
allora
![]() e
quindi
e
quindi
![]() ,
altrimenti ne sarebbe il minimo, ma allora
,
altrimenti ne sarebbe il minimo, ma allora ![]() e
pertanto
e
pertanto
![]() .
.
Ma allora
![]() e quindi
e quindi
![]() .
.
![]()
Dimostrazione.
Sia
![]() ,
e supponiamo per assurdo
che
,
e supponiamo per assurdo
che
![]() .
Allora per la proprietà di buon ordinamento A ha minimo n. Chiaramente
.
Allora per la proprietà di buon ordinamento A ha minimo n. Chiaramente ![]() in quanto
P(0) è vera. Inoltre se k<n allora
in quanto
P(0) è vera. Inoltre se k<n allora ![]() in quanto
in quanto ![]() ,
ma
allora dalla (2) segue che P(n) è vera e quindi
,
ma
allora dalla (2) segue che P(n) è vera e quindi ![]() ,
contraddicendo
il fatto che
,
contraddicendo
il fatto che ![]() .
.
![]()
Dimostrazione. Esistenza. Supponiamo dapprima che
![]() ,
ed usiamo il principio di
induzione nella seconda forma su n. Se n=0 basta prendere q=0 e r=0.
Supponiamo n>0 e che la tesi sia vera per ogni k<n. Se n<m basta prendere
q=0 e r=n, altrimenti sia k=n-m, dato che
,
ed usiamo il principio di
induzione nella seconda forma su n. Se n=0 basta prendere q=0 e r=0.
Supponiamo n>0 e che la tesi sia vera per ogni k<n. Se n<m basta prendere
q=0 e r=n, altrimenti sia k=n-m, dato che ![]()
![]() ,
quindi per
ipotesi di induzione esistono
,
quindi per
ipotesi di induzione esistono
![]() tali che
tali che
Supponiamo ora n<0 e m>0. Allora -n>0 e quindi per il caso
precedente si ha che esistono
![]() tali che -n=mq+r e
tali che -n=mq+r e
![]() .
E quindi n=m(-q)-r. Se r=0 abbiamo finito, se invece
0<r<m allora
.
E quindi n=m(-q)-r. Se r=0 abbiamo finito, se invece
0<r<m allora
![]() e
n=m(-q)-r=m(-q)-m+m-r=m(-1-q)+(m-r).
e
n=m(-q)-r=m(-q)-m+m-r=m(-1-q)+(m-r).
Sia infine m<0 allora -m>0, quindi per i due casi precedenti
esistono
![]() tali che
n=(-m)q+=m(-q)+r con
tali che
n=(-m)q+=m(-q)+r con
![]() .
.
Unicità. Supponiamo che n= mq + r e n=mq'+r' con
![]() .
Supponiamo
che
.
Supponiamo
che ![]() ,
allora
m(q-q')=r'-r e
quindi passando ai moduli si ha
,
allora
m(q-q')=r'-r e
quindi passando ai moduli si ha
![]() ,da cui
,da cui
![]() e quindi
e quindi
![]() ovvero q=q'. Ma
allora da
mq+r=mq'+r' segue che anche r=r'.
ovvero q=q'. Ma
allora da
mq+r=mq'+r' segue che anche r=r'.
![]()
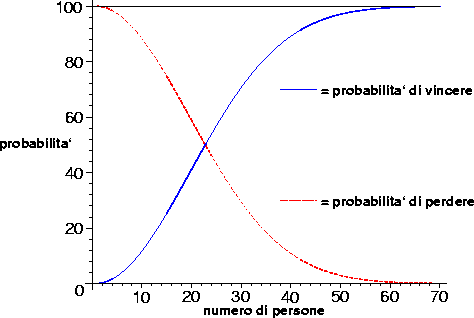
Storiella. Il professore di Matematica Discreta entra nell'aula, davanti ai suoi 60 studenti esclama: --Scommettiamo che due di voi hanno lo stesso compleanno?-- e aggiunge --se io perdo pago la cena a tutti, se vinco voi pagete una cena a me.--
Gli studenti accettano entusiasti la scommessa: --Male che vada ci rimettiamo 1000 lire ciascuno, ma in ogni caso-- pensano --è praticamente impossibile che il prof. vinca, siamo troppo pochi.--
Una rapida verifica e quindi la delusione: il professore, come ogni anno, si è guadagnato una cena.
Perché il prof. ha vinto? È soltanto una fortuna sfacciata, che gli consente di vincere ogni anno, o è qualcos'altro?
Formalizziamo la situazione. Associare ad ogni studente il proprio giorno di nascita è una funzione da un insieme X con 60 elementi (l'insieme degli studenti) in un insieme Y con 365 elementi (l'insieme dei possibili giorni di nascita, escludendo il caso degli anni bisestili). Il professore perde se tale funzione è iniettiva, vince altrimenti. Si tratta allora di contare il numero di funzioni iniettive, e dividerlo per il numero di funzioni, questo darà la probabilità di perdere la scommessa da parte del professore.
Questo, assieme al risultato dell'esercizio 1.12 (punto 2), ci dice che:
Se
![]() e
e
![]() la probabilità che una funzione
la probabilità che una funzione ![]() sia
iniettiva è pari a
sia
iniettiva è pari a
 |