Next: Lezione 8 (28 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 6 (14 marzo
Subsections
Definizione 7.1
Siano
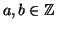
,
si dice che
a è congruo a
b modulo
n (in
simboli
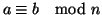
)
se
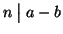
.
Dimostrazione.
1.
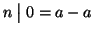 per ogni
per ogni
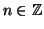 .
.
2. Se
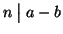 allora a-b=kn e quindi
b-a=(-k)n e quindi
allora a-b=kn e quindi
b-a=(-k)n e quindi
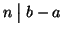 ossia
ossia
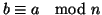 .
.
3. Se
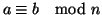 e
e
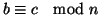 allora
a-b=kn e b-c=hn e quindi
a-c=a-b+b-c=kn+hn=(k+h)n e quindi
allora
a-b=kn e b-c=hn e quindi
a-c=a-b+b-c=kn+hn=(k+h)n e quindi
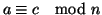 .
.

Ricordiamo la definizione di relazione d'equivalenza su un insieme.
Osservazione 7.4
La proposizione precedente può essere allora rienunciato dicendo che
la relazione di congruenza modulo n è una relazione d'equivalenza su
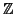
.
Definizione 7.5
Siano
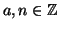
,
si chiama classe di congruenza di
a modulo
n l'insieme
Indicheremo
![$\mathbb Z\big/\mathchoice
{{}_{\!\displaystyle {}n\mathbb Z}}
{{}_{\!\textsty...
...scriptstyle {}n\mathbb Z}}=\big\{\left[a\right]_n\bigm\vert a\in\mathbb Z\big\}$](img474.gif)
Osservazione 7.6
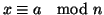
se e solo se
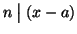
se e solo se esiste
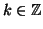
tale che
x-
a=
kn se e solo se esiste
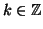
tale che
x=
a+
kn e quindi
Dimostrazione.
1. Segue dalla proprietà
riflessiva.
2. Se
![$\left[a\right]_n=\left[b\right]_n$](img480.gif) in particolare
in particolare
![$b\in\left[b\right]_n=\left[a\right]_n$](img482.gif) e quindi
e quindi
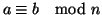 .
Viceversa sia
.
Viceversa sia
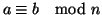 .
Se
.
Se
![$x\in \left[a\right]_n$](img483.gif) allora
allora
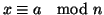 ;
per la
proprietà transitiva
;
per la
proprietà transitiva
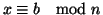 ossia
ossia
![$x\in\left[b\right]_n$](img485.gif) .
Analogamente se
.
Analogamente se
![$x\in\left[b\right]_n$](img485.gif) allora
allora
![$x\in \left[a\right]_n$](img483.gif) e quindi le due
classi coincidono.
e quindi le due
classi coincidono.
3. Se
![$x\in\left[a\right]_n\cap\left[b\right]_n$](img486.gif) allora
allora
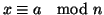 e
e
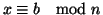 ,
usando le proprietà
simmetrica e transitiva si ha
allora che
,
usando le proprietà
simmetrica e transitiva si ha
allora che
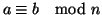 e quindi, per la (2), appena
dimostrata,
e quindi, per la (2), appena
dimostrata,
![$\left[a\right]_n=\left[b\right]_n$](img480.gif) .
.

In generale data una relazione d'equivalenza su un insieme
Proposizione 7.8
Se
n>0 e
r è il resto della divisione euclidea di
a per
n allora
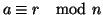
.
Dimostrazione.
a=nq+r quindi
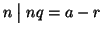 .
.

Corollario 7.9
Se
n>0 allora
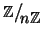
ha esattamente
n elementi.
Dimostrazione.
Da 7.8 e dalla 2 di
7.7 segue immediatamente che l'insieme in questione
ha al più n elementi e precisamente
![$\left[0\right]_n,\left[1\right]_n,\dots,\left[n-1\right]_n$](img490.gif) .
D'altra parte se
.
D'altra parte se
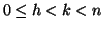 allora 0<k-h<n e quindi
allora 0<k-h<n e quindi
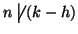 e quindi (sempre
per la 2 di 7.7)
e quindi (sempre
per la 2 di 7.7)
![$\left[h\right]_n\ne\left[k\right]_m$](img493.gif) .
.

Successioni di tipo Fibonacci
La successione di Fibonacci è la successione 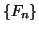 così
definita
così
definita
Esercizio 7.1
Si provi che
(
Fn+1,
Fn)=1 per ogni
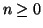
.
Soluzione
Esercizio 7.3
Si provi che dette
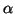
e
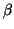
le radici del polinomio
x2-3
x+2,
allora le successioni
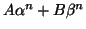
al variare di
A e
B sono tutte
e sole le successioni tali che
xn+2=3xn+1-2
Soluzione
Esercizio 7.4
Si determini la successione tale che
Soluzione
In effetti si può dimostrare il seguente
Teorema 7.10
Siano
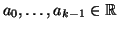
(o anche
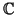
), tali che il polinomio
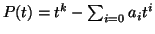
ammette
k radici distinte
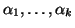
,
allora le successioni del tipo
sono tutte e sole le successioni tali che
In più, dati numeri
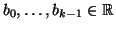
(
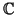
)
esiste un'unica di
tali successioni tale che



Next: Lezione 8 (28 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 6 (14 marzo
Domenico Luminati
2000-06-14
![]() per ogni
per ogni
![]() .
.
![]() allora a-b=kn e quindi
b-a=(-k)n e quindi
allora a-b=kn e quindi
b-a=(-k)n e quindi
![]() ossia
ossia
![]() .
.
![]() e
e
![]() allora
a-b=kn e b-c=hn e quindi
a-c=a-b+b-c=kn+hn=(k+h)n e quindi
allora
a-b=kn e b-c=hn e quindi
a-c=a-b+b-c=kn+hn=(k+h)n e quindi
![]() .
.
![]()
![]() in particolare
in particolare
![]() e quindi
e quindi
![]() .
Viceversa sia
.
Viceversa sia
![]() .
Se
.
Se
![]() allora
allora
![]() ;
per la
proprietà transitiva
;
per la
proprietà transitiva
![]() ossia
ossia
![]() .
Analogamente se
.
Analogamente se
![]() allora
allora
![]() e quindi le due
classi coincidono.
e quindi le due
classi coincidono.
![]() allora
allora
![]() e
e
![]() ,
usando le proprietà
simmetrica e transitiva si ha
allora che
,
usando le proprietà
simmetrica e transitiva si ha
allora che
![]() e quindi, per la (2), appena
dimostrata,
e quindi, per la (2), appena
dimostrata,
![]() .
.
![]()
![]() .
.
![]()
![]() .
D'altra parte se
.
D'altra parte se
![]() allora 0<k-h<n e quindi
allora 0<k-h<n e quindi
![]() e quindi (sempre
per la 2 di 7.7)
e quindi (sempre
per la 2 di 7.7)
![]() .
.
![]()
![]() così
definita
così
definita