Next: Lezione 9 (31 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 7 (27 marzo
Subsections
Somma e prodotto di classi di congruenza
Dimostrazione.
(1). Se
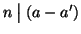 e
e
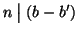 allora
allora
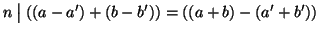 .
.
(2). Esistono
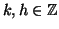 tali che a=a'+kn e b=b'+hn, ma
allora, moltiplicando membro a membro si ottiene
ab=a'b'+a'hn+b'kn+hkn2=a'b'+n(a'h+b'k+hkn) e quindi la tesi.
tali che a=a'+kn e b=b'+hn, ma
allora, moltiplicando membro a membro si ottiene
ab=a'b'+a'hn+b'kn+hkn2=a'b'+n(a'h+b'k+hkn) e quindi la tesi.

Osservazione 8.2
La proposizione precedente permette di definire le operazioni di
somma e prodotto tra classi modulo
n. Ponendo
si ottengono delle buone definizioni. Infatti se
![$\left[a\right]_n=\left[a'\right]_n$](img520.gif)
e
![$\left[b\right]_n=\left[b'\right]_n$](img521.gif)
allora per la
2 di
7.7 si ha che

e
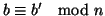
e quindi
per la
proposizione precedente si ha che
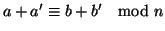
e
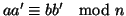
e quindi di nuovo per la
2 di
7.7 si ha che
![$\left[a+b\right]_n=\left[a'+b'\right]_n$](img524.gif)
e
![$\left[ab\right]_n=\left[a'b'\right]_n$](img525.gif)
.
Nel seguito, quando parleremo di classi di congruenza e di operazioni tra esse,
potrà succedere che, nella notazione, confonderemo la classe con uno dei suoi
rappresentanti. Sarà chiaro dal contesto a cosa ci si starà riferendo. Ad
esempio useremo indifferentemente una delle tre espressioni
per indicare lo stesso concetto.
Osservazione 8.3
L'esercizio precedente, mostra che le operazioni tra classi di congruenza
godono delle stesse proprietà di cui godono le operazioni tra interi.
Attenzione però a due importanti differenze:
- 1.
- Ci possono essere classi diverse da 0 che moltiplicate tra loro danno
0, ad esempio
- 2.
- Se n>0 allora
equazioni lineari modulo n
Dimostrazione.
Se
 allora
allora
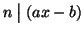 quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
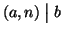 .
.
Viceversa supponiamo che
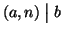 .
Siano
.
Siano
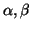 tali che
tali che
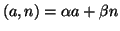 , e sia k tale che
b = k(a,n) allora
, e sia k tale che
b = k(a,n) allora
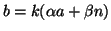 e quindi
e quindi
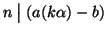 ,
ossia
,
ossia
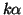 è una soluzione della congruenza.
è una soluzione della congruenza.

Osservazione 8.5
La dimostrazione precedente dà un metodo operativo per trovare una soluzione
della congruenza, basta usare l'algoritmo di Euclide per determINARE
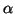
e
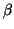
in modo che
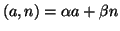
.
Esercizio 8.2
Si provi che quando ha soluzione, la congruenza

è
equivalente alla congruenza
essendo
a'=
a/(
a,
n),
b'=
b/(
a,
n),
n'=
n/(
a,
n).
Soluzione
Il teorema cinese del resto
Teorema 8.6 (Cinese del resto)
Il sistema di congruenze
ha soluzione se e solo se
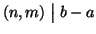
.
Se
c è una soluzione del sistema, allora gli elementi di
![$\left[c\right]_{[n,m]}$](img549.gif)
sono tutte e sole le soluzioni del sistema (i.e. le soluzioni sono
tutte e sole della forma
c+
k[
n,
m] al variare di
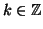
).
Dimostrazione.
Sia c una soluzione del sistema allora esistono
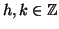 tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
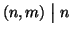 e
e
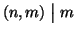 si ha che
si ha che
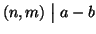 .
Viceversa, supponiamo che
.
Viceversa, supponiamo che
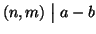 ,
allora esistono
,
allora esistono
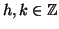 tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
Sia
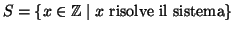 .
Dobbiamo provare
che se c è una soluzione allora
.
Dobbiamo provare
che se c è una soluzione allora
![$S=\left[c\right]_{[n,m]}$](img555.gif) .
.
![$S\subseteq\left[c\right]_{[n,m]}$](img556.gif) .
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
.
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
Ma allora
![$[n,m]\mathrel{\big\vert}c-c'$](img558.gif) ossia
ossia
![$c'\cong c\quad{\rm mod}\ [n,m]$](img559.gif) ovvero
ovvero
![$c'\in\left[c\right]_{[n,m]}$](img560.gif) .
.
![$\left[c\right]_{[n,m]}\subseteq S$](img561.gif) .
Sia
.
Sia
![$c'\in\left[c\right]_{[n,m]}$](img560.gif) ,
ovvero
c'=c+h[n,m]. Dal fatto che
,
ovvero
c'=c+h[n,m]. Dal fatto che
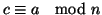 e che
e che
![$h[n,m]\cong 0\quad{\rm mod}\ n$](img563.gif) segue che
segue che
![$c'=c+h[n,m]\cong a \quad{\rm mod}\ n$](img564.gif) .
In modo analogo si ha che
.
In modo analogo si ha che
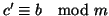 e
quindi che
e
quindi che 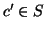 .
.

Esercizio 8.3
Siano
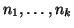
interi a due a due primi tra loro. Si provi che il
sistema di congruenze
ammette soluzione e che se
c è una soluzione, tutte le altre sono del tipo
![$c + k n_1\cdot\dots\cdot n_k]$](img569.gif)
.
Soluzione
Esercizio 8.4
Siano
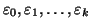
le cifre della espressione decimale del numero
n. Si provi che
- 1.
-
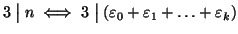
- 2.
-
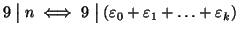
- 3.
-
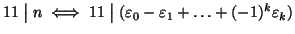
Soluzione



Next: Lezione 9 (31 marzo
Up: Matematica Discreta (II modulo)
Previous: Lezione 7 (27 marzo
Domenico Luminati
2000-06-14
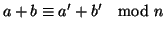 ;
;
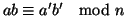 .
.
![]() e
e
![]() allora
allora
![]() .
.
![]() tali che a=a'+kn e b=b'+hn, ma
allora, moltiplicando membro a membro si ottiene
ab=a'b'+a'hn+b'kn+hkn2=a'b'+n(a'h+b'k+hkn) e quindi la tesi.
tali che a=a'+kn e b=b'+hn, ma
allora, moltiplicando membro a membro si ottiene
ab=a'b'+a'hn+b'kn+hkn2=a'b'+n(a'h+b'k+hkn) e quindi la tesi.
![]()
![\begin{eqnarray*}\left[a\right]_n+\left[b\right]_n & = & \left[a+b\right]_n
\\
\left[a\right]_n \left[b\right]_n & = & \left[ab\right]_n
\end{eqnarray*}](img519.gif)
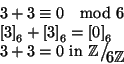
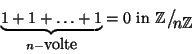
![]() allora
allora
![]() quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
quindi esiste k tale che
ax-b=kn ossia b=ax-kn e quindi
![]() .
.
![]() .
Siano
.
Siano
![]() tali che
tali che
![]() , e sia k tale che
b = k(a,n) allora
, e sia k tale che
b = k(a,n) allora
![]() e quindi
e quindi
![]() ,
ossia
,
ossia
![]() è una soluzione della congruenza.
è una soluzione della congruenza.
![]()
![]() tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
tali che
c=a+hn=b+km e quindi a-b=km-hn. Ma allora dal fatto che
![]() e
e
![]() si ha che
si ha che
![]() .
Viceversa, supponiamo che
.
Viceversa, supponiamo che
![]() ,
allora esistono
,
allora esistono
![]() tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
tali che
a-b=hn+km. Ma allora a-hn=b+kn, detto quindi
c=a-hn=b+kn, si ha
evidentemente che c risolve entrambe le congruenze.
![]() .
Dobbiamo provare
che se c è una soluzione allora
.
Dobbiamo provare
che se c è una soluzione allora
![]() .
.
![]() .
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
.
Sia c' un'altra soluzione, allora
c=a+hn=b+km e
c'=a+h'n=b+k'm e quindi sottraendo si ha
![]() .
Sia
.
Sia
![]() ,
ovvero
c'=c+h[n,m]. Dal fatto che
,
ovvero
c'=c+h[n,m]. Dal fatto che
![]() e che
e che
![]() segue che
segue che
![]() .
In modo analogo si ha che
.
In modo analogo si ha che
![]() e
quindi che
e
quindi che ![]() .
.
![]()