

Next: Lezione 15 (7 maggio
Up: Matematica Discreta
Previous: Lezione 13 (3 aprile
Subsections
Definizione 14.1
Un grafo
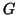
è una coppia ordinata
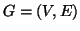
dove
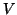
è un insieme non
vuoto detto insieme dei
vertici del grafo ed
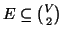
è detto l'insieme dei
lati. Se
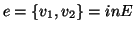
,
si dirà che il lato
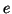 congiunge
congiunge i due vertici
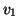
e
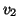
e si
dirà anche che
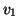
e
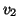
sono gli
estremi del lato
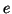
.
Se 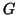 è un grafo, indicheremo con
è un grafo, indicheremo con 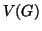 l'insieme dei suoi vertici e con
l'insieme dei suoi vertici e con
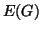 l'insieme dei suoi lati, ovvero
l'insieme dei suoi lati, ovvero 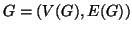 .
.
Se 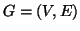 è un grafo e
è un grafo e 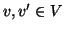 si dirà
che
si dirà
che 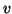 e
e 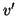 sono adiacenti o che
sono adiacenti o che 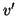 è vicino a
è vicino a 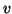 se
se
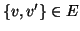 (cfr. esercizio 14.2).
(cfr. esercizio 14.2).
Spesso i grafi sono rappresentati graficamente mediante dei punti a
rappresentare i vertici e delle linee congiungenti due vertici a rappresentare i
lati. Ad esempio in figura 1 sono rappresentati i
grafi 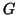 e
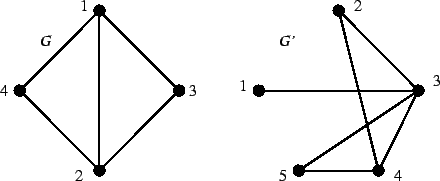
e 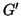 definiti da
definiti da
Figura 1:
Esempi di grafi
 |
Osservazione 14.2
Se
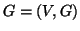
è un grafo, l'essere adiacenti, definisce una relazione su
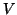
detta
relazione d'adiacenza che denoteremo con
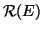
. Ossia:
Tale relazione risulta essere oviamente
- simmetrica ossia
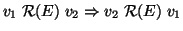
- antiriflessiva ossia
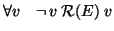
Viceversa, data una relazione simmetrica e antiriflessiva 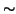 sull'insieme
sull'insieme
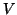 , l'insieme
, l'insieme
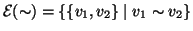 è un sottinsieme
di
è un sottinsieme
di 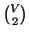 , e quindi
, e quindi
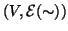 è un grafo.
è un grafo.
Dimostrazione.
(1). Dalle definizioni si ha immediatamente che
e quindi
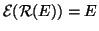 .
.
(2).
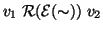 se e solo se
se e solo se
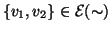 e
per definizione di
e
per definizione di
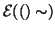 questo è vero se e solo se o
questo è vero se e solo se o 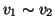 o
o
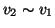 . Dato che la relazione
. Dato che la relazione 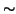 è simmetrica, ciò equivale a
dire
è simmetrica, ciò equivale a
dire 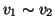 .
.

Osservazione 14.4
La proposizione precedente prova che dare un grafo i cui vertici sono
l'insieme
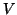
è equivalente a dare una relazione simmetrica e
antiriflessiva su
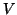
.
Osservazione 14.5
Si osservi che affinchè
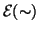
sia l'insieme dei lati di un grafo è
necessario soltanto che
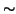
sia antiriflessiva. La simmetria di
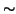
è necessaria però per provare la seconda proprietà della proposizione
precedente.
Esercizio 14.1
Provare nel dettaglio quanto asserito nell'osservazione
14.2.
Soluzione
Esercizio 14.2
Sia
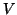
un insieme, e sia
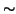
una relazione antiriflessiva su
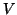
. Si
provi che se
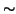
non è simmetrica allora
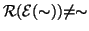
.
Si produca anche un esempio di relazione 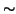 su un insieme tale che
su un insieme tale che
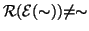 .
.
Soluzione
Definizione 14.6
Un
grafo diretto è una coppia
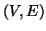
dove

è
una relazione binaria su
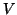
.
Diamo alcuni esempi di grafi notevoli, per i quali esiste anche una notazione
standard.
Per ogni
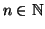 indicheremo con
indicheremo con 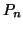 il grafo tale che
il grafo tale che
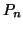 è detto il cammino di lunghezza
è detto il cammino di lunghezza 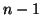 (i.e. ha
(i.e. ha 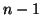 lati).
lati).
Indicheremo con 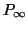 il grafo
il grafo
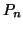 è detto il cammino infinito.
è detto il cammino infinito.
Per ogni
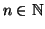 ,
, 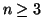 indicheremo con
indicheremo con 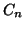 il grafo tale che
il grafo tale che
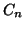 è detto il ciclo di lunghezza
è detto il ciclo di lunghezza 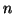 (i.e. ha
(i.e. ha 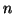 lati e
lati e 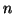 vertici).
vertici).
Per ogni
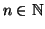 , indicheremo con
, indicheremo con 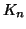 il grafo tale che
il grafo tale che
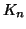 è detto il grafo completo su
è detto il grafo completo su 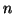 vertici (i.e. ha tutti i lati
possibili che congiungono i suoi
vertici (i.e. ha tutti i lati
possibili che congiungono i suoi 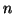 vertici).
vertici).
Per ogni
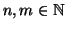 , indicheremo con
, indicheremo con 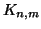 il grafo tale che
il grafo tale che
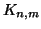 è detto il grafo completo bipartito su
è detto il grafo completo bipartito su 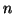 ed
ed 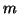 vertici
(i.e. ha tutti i lati possibili che congiungono i suoi primi
vertici
(i.e. ha tutti i lati possibili che congiungono i suoi primi 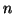 vertici con
gli altri
vertici con
gli altri 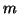 ).
).
Definizione 14.8
Siano
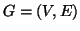
e
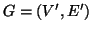
due grafi, si dirà che
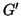
è
sottografo di
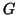
se e solo se
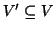
e
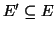
.
Definizione 14.9
Sia
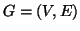
un grafo e sia
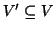
, chiameremo il
sottografo
indotto da
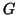
su
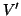
il grafo
![$G[V']=(V',E\cap {V' \choose 2})$](img1181.gif)
.
Detto in altri termini nel sottografo indotto si mettono tutti i lati del grafo
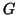 che congiungono vertici di
che congiungono vertici di 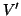 .
.
Esercizio 14.3
Si provi che
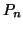
è sottografo di
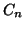
per ogni
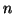
.
Soluzione
Esercizio 14.4
Sia
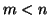
e sia
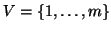
. Si determini il sottografo indotto da
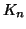
su
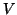
.
Soluzione
Esercizio 14.5
Siano
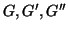
grafi e si provi che se
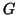
è sottografo di
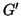
e
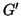
è
sottografo di
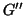
allora
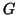
è sottografo di
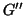
.
Soluzione
Morfismi ed isomorfismo di grafi
Osservazione 14.11
Osserviamo che la condizione di essere un morfismo può essere espressa
anche dicendo che
dove con
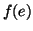
si intende l'immagine mediante
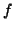
del sottinsieme
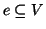
e con
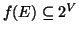
l'insieme di tali immagini al
variare di
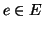
. In simboli
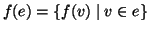
(ovvero se
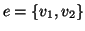
allora
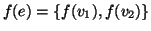
), e
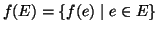
.
Per questo motivo un morfismo sarà denotato anche con
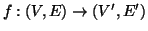 .
.
Osservazione 14.12
Se
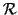
e
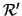
denotano le relazioni di adiacenza dei grafi
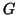
e
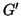
, la
proprietà di essere un morfismo si rienuncia in termini di
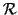
e
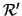
ed in questa forma può essere estesa ai grafi diretti.
Definizione 14.13
Un morfismo
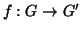
si dice un
isomorfismo se
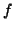 è bigettiva
è bigettiva
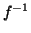 è a sua volta un morfismo.
è a sua volta un morfismo.
In tal caso i due grafi 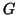 e
e 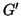 si direnno isomorfi, e si
denoterà con
si direnno isomorfi, e si
denoterà con 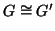 .
.
Proposizione 14.14
Siano
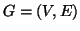
e
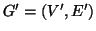
due grafi. Una funzione
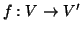
è un
isomorfismo se e solo se
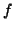 è bigettiva
è bigettiva
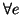
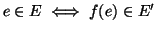 .
.
Dimostrazione.
Supponiamo che 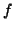 sia un isomorfismo, allora per definizione
sia un isomorfismo, allora per definizione 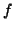 è
bigettiva. Dal fatto che
è
bigettiva. Dal fatto che 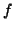 è un morfismo segue che se
è un morfismo segue che se
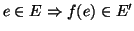 , dal fatto che
, dal fatto che 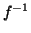 è un morfismo segue allora che se
è un morfismo segue allora che se 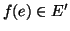 allora
allora
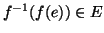 , ma
, ma
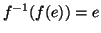 e quindi è verificata la
(2).
e quindi è verificata la
(2).
Viceversa dalla (2) segue che se 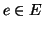 allora
allora 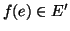 e quindi
e quindi 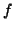 è
un morfismo. Proviamo che
è
un morfismo. Proviamo che 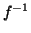 è a sua volta un morfismo. Sia
è a sua volta un morfismo. Sia 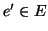 ,
dato che
,
dato che 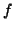 è bigettiva allora esiste
è bigettiva allora esiste
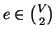 tale che
tale che 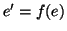 . Ma allora dalla (2) segue che
. Ma allora dalla (2) segue che
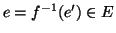 e quindi la tesi.
e quindi la tesi.

Esercizio 14.6
Si provi che
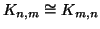
per ogni
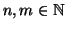
.
Soluzione
Esercizio 14.7
Siano
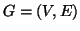
e
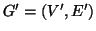
due grafi. Si provi che se
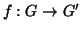
è un
morfismo tale che
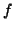
è iniettiva e
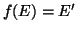
allora
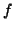
è un isomorfismo.
Soluzione
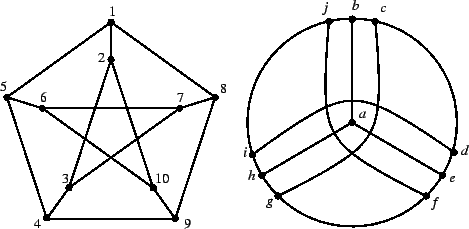
Esercizio 14.9
Si provi che i due grafi rappresentati in figura
3 sono tra
loro isomorfi.
Figura:
I grafi di esercizio 14.9
 |
Soluzione
Esercizio 14.10
Dire se i due grafi in figura
4 sono isomorfi oppure no.
Figura 4:
I grafi dell'esercizio 14.10
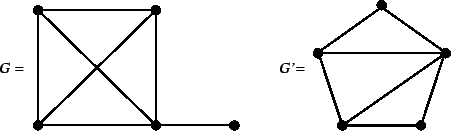 |
Soluzione
Esercizio 14.11
Provare che i due grafi in figura
5 non sono isomorfi.
Figura 5:
I grafi dell'esercizio 14.11
 |
Soluzione
Esercizio 14.12
Sia
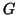
il grafo dato dai vertici e dagli spigoli di un cubo e sia
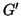
il
grafo tale che
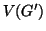
sia l'insieme delle parole di tre lettere nell'alfabeto
di due lettere
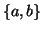
ed in cui due parole sono congiunte da un lato se e
solo se differiscono per una lettera soltanto. Si provi che
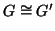
.
Soluzione


Next: Lezione 15 (7 maggio
Up: Matematica Discreta
Previous: Lezione 13 (3 aprile
Luminati Domenico
2002-06-07
![]() è un grafo e
è un grafo e ![]() si dirà
che
si dirà
che ![]() e
e ![]() sono adiacenti o che
sono adiacenti o che ![]() è vicino a
è vicino a ![]() se
se
![]() (cfr. esercizio 14.2).
(cfr. esercizio 14.2).
![]() e
e ![]() definiti da
definiti da
![]() sull'insieme
sull'insieme
![]() , l'insieme
, l'insieme
![]() è un sottinsieme
di
è un sottinsieme
di ![]() , e quindi
, e quindi
![]() è un grafo.
è un grafo.![]() se e solo se
se e solo se
![]() e
per definizione di
e
per definizione di
![]() questo è vero se e solo se o
questo è vero se e solo se o ![]() o
o
![]() . Dato che la relazione
. Dato che la relazione ![]() è simmetrica, ciò equivale a
dire
è simmetrica, ciò equivale a
dire ![]() .
.
![]()
![]() su un insieme tale che
su un insieme tale che
![]() .
.
![]() e
e ![]() di un grafo diretto ci possono essere entrambi i lati
di un grafo diretto ci possono essere entrambi i lati
![]() e
e ![]() , e si possono avere anche lati del tipo
, e si possono avere anche lati del tipo ![]() (vedi
figura 2).
(vedi
figura 2).
![]() anche
anche ![]() ) e antiriflessivo (i.e.
) e antiriflessivo (i.e. ![]() per ogni
per ogni ![]() ). In altri termini la
nozione di grafo diretto è una estensione di quella di grafo.
). In altri termini la
nozione di grafo diretto è una estensione di quella di grafo.![]() indicheremo con
indicheremo con ![]() il grafo tale che
il grafo tale che
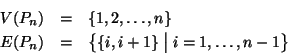
![]() il grafo
il grafo
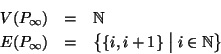
![]() ,
, ![]() indicheremo con
indicheremo con ![]() il grafo tale che
il grafo tale che
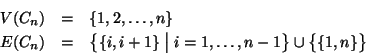
![]() , indicheremo con
, indicheremo con ![]() il grafo tale che
il grafo tale che
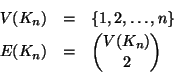
![]() , indicheremo con
, indicheremo con ![]() il grafo tale che
il grafo tale che
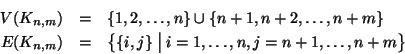
![]() .
.![]() e
e ![]() si direnno isomorfi, e si
denoterà con
si direnno isomorfi, e si
denoterà con ![]() .
.![]() sia un isomorfismo, allora per definizione
sia un isomorfismo, allora per definizione ![]() è
bigettiva. Dal fatto che
è
bigettiva. Dal fatto che ![]() è un morfismo segue che se
è un morfismo segue che se
![]() , dal fatto che
, dal fatto che ![]() è un morfismo segue allora che se
è un morfismo segue allora che se ![]() allora
allora
![]() , ma
, ma
![]() e quindi è verificata la
(2).
e quindi è verificata la
(2).
![]() allora
allora ![]() e quindi
e quindi ![]() è
un morfismo. Proviamo che
è
un morfismo. Proviamo che ![]() è a sua volta un morfismo. Sia
è a sua volta un morfismo. Sia ![]() ,
dato che
,
dato che ![]() è bigettiva allora esiste
è bigettiva allora esiste
![]() tale che
tale che ![]() . Ma allora dalla (2) segue che
. Ma allora dalla (2) segue che
![]() e quindi la tesi.
e quindi la tesi.
![]()