Lezione 15 (7 maggio 2001 h. 9.30-10.30)

Una stima del numero di grafi non isomorfi su $n$ vertici

Sia $V=\{1,2,\dots,n\}$ e indichiamo con ${\cal G}_n$ l'insieme dei grafi che hanno $V$ come insieme dei vertici. Dall'esercizio 14.8 segue che $\oldcong$ è una relazione d'equivalenza su ${\cal G}_n$. Indichiamo con $g_n=\left\vert{\cal G}_n\big/\mathchoice {{}_{\!\displaystyle {}\oldcong }} {... ...!\scriptstyle {}\oldcong }} {{}_{\!\scriptscriptstyle {}\oldcong }}\right\vert$.

In parolo povere $g_n$ è il massimo numero di grafi di ${\cal G}_n$ tra loro non isomorfi. ovvero se si è interessati a sapere quanti sono i grafi essenzialmente diversi con vertici $V$ il numero interessante è $g_n$.

Proposizione 15.1   Con le notazioni appena introdotte si ha che

$$\frac{n^2}{2}\Big( 1 - \frac{1}{n} - \frac{2}{n}\log_2(n)\B... ... \le \log_2(g_n) \le \frac{n^2}{2}\Big( 1 - \frac{1}{n}\Big )$$

Dimostrazione.  L'insieme ${\cal G}_n$ è evidentemente in bigezione con $2^{{V \choose 2}}$ e quindi

$$2^{{n \choose 2}}=\left\vert{\cal G}_n\right\vert,$$

in particolare allora $g_n\le \left\vert{\cal G}_n\right\vert = 2^{{n \choose 2}}$, da cui passando al $\log_2$ si ha

$$\log_2(g_n) \le {n \choose 2} = \frac{n^2}{2}\Big( 1 - \frac{1}{n}\Big ).$$

Dato che le classi di equivalenza formano una partizione di ${\cal G}_n$,

$$\left\vert{\cal G}_n\right\vert = \sum_{x\in{\cal G}_n\big/\... ...}_{\!\scriptscriptstyle {}\oldcong }}} \left\vert x\right\vert$$

ossia la cardinalità di ${\cal G}_n$ è la somma delle cardinalità di ciascuna classe d'isomorfismo, e quindi

$$2^{{n \choose 2}} = \sum_{x\in{\cal G}_n\big/\mathchoice {... ...}_{\!\scriptscriptstyle {}\oldcong }}} \left\vert x\right\vert$$ (8)

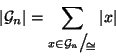
Osserviamo ora che dato un grafo $G\in{\cal G}_n$, il numero di grafi di ${\cal G}_n$ a lui isomorfi è al massimo $n!$ (ossia il numero di funzioni bigettive $V\to V$). Ma allora per ogni $x\in {\cal G}_n\big/\mathchoice {{}_{\!\displaystyle {}\oldcong }} {{}_{\!\te... ... }} {{}_{\!\scriptstyle {}\oldcong }} {{}_{\!\scriptscriptstyle {}\oldcong }}$ si ha che $\left\vert x\right\vert\le n!$. Da ciò e dalla (8) si deduce allora che

$$2^{{n \choose 2}} \le \sum_{x\in{\cal G}_n\big/\mathchoice ... ...} {{}_{\!\scriptscriptstyle {}\oldcong }}\right\vert =g_n n!.$$

e quindi

$$g_n \ge \frac{2^{{n \choose 2}}}{n!}.$$

Pasando al $\log_2$ si ha che

$$\log_2(g_n) \ge \log_2\big(\frac{2^{{n \choose 2}}}{n!}\big... ... \choose 2}}\big) - \log_2({n!}) ={n \choose 2} - \log_2({n!})$$

D'altra parte $n!\le n^n$, quindi $\log_2({n!})\le \log_2({n^n})=n\log_2(n)$ e perciò

$$\log_2(g_n) \ge {n \choose 2} -n\log_2(n) = \frac{n(n-1)}{2... ...n) = \frac{n^2}{2}\Big(1-\frac{1}{n}-\frac{2}{n}\log_2(n)\Big)$$

    $\square$

Osservazione 15.2   La stima precedente prova $\log_2(g_n)$ ha lo stesso ordine di infinito di $n^2/2$, dato che quandi $n$ è grande, il numero $1-1/n-2\log_2(n)/n$ è molto vicino a $1$. Questo prova che il problema di classificare i grafi a meno di isomorfismo è intrinsecamente difficile (anche da un punto di vista meramente computazionale) dato che il numero di classi non isomorfe è esponenziale nel numero dei vertici con esponente che ha lo stesso ordine di infinito di $n^2/2$.

Passeggiate, cammini e cicli

Definizione 15.3   Sia $G=(V,E)$ un grafo una successione finita di vertici $(v_0,\dots,v_n)$ sarà detta

• passeggiata se $\{v_i,v_{i+1}\}\in E$ per ogni $i=0,\dots,n-1$
• cammino se è una passeggiata e $v_i\ne v_j$ per ogni $i\ne j$.
• ciclo se è una passeggiata e $v_i\ne v_j$ per ogni $i\ne j$ a parte $v_0=v_n$.

Diremo che la passeggiata $P=(v_0,\dots, v_n)$ ha lunghezza $n$ ed indicheremo con $\ell(P)$ la lunghezza di $P$.

Proposizione 15.4   Sia $G$ un grafo e sia $(_0,\dots, v_n)$ un cammino in $G$ allora il grafo $G'$ definito da:

• $V(G')=\{v_0,\dots,v_n\}$
• $E(G')=\big\{\{v_i,v_{i+1}\}\bigm\vert i=0,\dots,n-1\big\}$

è un sottografo di $G$ isomorfo a $P_n$.

Dimostrazione.  Esercizio.     $\square$

Proposizione 15.5   Sia $G$ un grafo e sia $(v_0,\dots,v_n)$ un ciclo in $G$ allora il grafo $G'$ definito da:

• $V(G')=\{v_0,\dots,v_{n-1}\}$
• $E(G')=\big\{\{v_i,v_{i+1}\}\bigm\vert i=0,\dots,n-1\big\}\cup\big\{\{v_n,v_0\}\big\}$

è un sottografo di $G$ isomorfo a $C_n$.

Dimostrazione.  Esercizio.     $\square$

Osservazione 15.6   In effetti è facile vedere che dare un cammino o un ciclo in un grafo è equivalente a dare un sottografo isomorfo a $P_n$ o $C_n$ per qualche $n$.

La relazione di essere congiungibili

Definizione 15.7   Sia $G=(V,E)$ e siano $v,w\in V$. Diremo che $v$ e $w$ sono congiungibili con un cammino [risp. una passeggiata] se e siste un cammino [risp. una passeggiata] $(v_0,\dots,v_n)$ tale che $v_0=v$ e $v_n=w$.

Proposizione 15.8   Due punti sono congiungibili mediante un cammino se e solo se lo sono mediante una passeggiata.

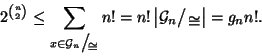
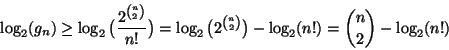
Dimostrazione.  Dato che un cammino è una passeggiata, se due vertici sono congiungibili mediante un cammino lo sono anche mediante una passeggiata.

Viceversa supponiamo che tra due vertici $u$ e $v$ esista una passeggiata. Sia ${\cal P}=\{P\mid P\hbox{\rm { \\lq e una passegiiata tra }}u\hbox{\rm { e }}v\}$ e sia $A=\{\ell(P)\mid P\in {\cal P}\}$. Dato che $u$ e $v$ sono congiungibili da una passeggiata, l'insieme ${\cal P}$ è non vuoto e quindi anche $A\ne\varnothing$. Ma allora per la proprietà di buon ordinamento dei numeri naturali, ha minimo, ovvero esiste una passeggiata $P_0$ da $u$ a $v$ che ha lunghezza minima nel senso che

$$\forall P\in {\cal P}\quad \ell(P_0) \le \ell(P).$$

Proviamo che $P_0$ deve essere un cammino. Sia $P_0=(v_0,\dots,v_m)$, se per assurdo $P_0$ non fosse un cammino esisterebbero $i<j$ tali che $v_i=v_j$, si consideri $P_1=(v_0,\dots,v_i,v_{j+1},\dots,v_m)$. $P_1$ è una passeggiata, infatti, dato che $P_0$ è una passeggiata, $v_h,v_{h+1}\}\in{\cal E}(()G)$ per ogni $0\le h <m$, e dato che $v_i=v_j$, $\{v_i,v_{j+1}\}=\{v_i,v_{i+1}\}\in E(G)$. $P_1$ congiunge $u$ a $v$, dato che $v_0=u$ e $v_m=v$ ed essendo, quindi $P_1\in {\cal P}$. Ma $\ell(P_1)=m-(j-i)<m$ e ciò contraddice la minimalità di $P_0$.     $\square$

Questa proposizione dice quindi che le due nozioni di congiungibilità che abbiamo sopra definito, sono in realtà la stessa. D'ora in poi diremo semplicemente che due punti sono congiungibili per dire che lo sono in uno dei due sensi (e quindi in tutti due i sensi) della definizione precedente.

Proposizione 15.9   Le relazione di essere congiungibli è una relazione d'equivalenza.

Dimostrazione.  Indichiamo con $\sim$ la relazione di congiungibilità (i.e. $u\sim v$ se e solo se $u$ è congiungibile a $v$). Dobbiamo provare che la relazione di essere congiungibili$\sim$ è riflessiva, simmetrica e transitiva.

La relazione è riflessiva. Invfatti per ogni $v\in V(G)$ , $(v)$ è un cammino che congiunge $v$ a $v$, quindi per ogni $v$ si ha che $v\sim v$.

La relazione è simmetrica. Se $u\sim v$ allora esiste una passeggiata $P=(v_0,\dots, v_n)$ tale che $u=v_0$ e $v=v_n$. Ma allora $P'=(v_n,v_{n-1},\dots,v_0)$ è una passeggiata (due vertici consecutivi in $P'$ sono adiacenti, dato che sono consecutivi --anche se in ordine scambiato-- in $P$) il cui primo vertice è $v$ e l'ultimo è $u$, ovvero

La relazione è transitiva. Se $u\sim v$ e $v\sim w$ allora esistono due passeggiate $P_1=(v_0,\dots,v_n)$ e $P_2=(u_0,\dots,u_m)$ tali che $u=v_0$, $v=u_n=u_0$ e $w=u_m$. Sia $Q=(v_0,\dots,v_n,u_1,\dots,u_m)$; $Q$ è una passeggiata dato che vertici consecutivi in $Q$ sono consecutivi o in $P$ o in $P'$ (si osservi che essendo $v_n=u_0$ si ha che $v_n$ e $u_1$ sono consecutivi in $P'$), d'atra parte il primo e l'ultimo vertice di $Q$ sono $v$ e $w$, quindi $v\tilde w$.     $\square$