

Next: Lezione 8 (21 marzo
Up: Matematica Discreta
Previous: Lezione 6 (14 marzo
Subsections
Operazioni tra cardinalità
Sebbene non abbiamo dato la definizione di cardinalità di un insieme, (abbiamo
dato significato al simbolo
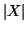 solo nel caso finito), con una serie di esercizi, vediamo
come si possano ugualmente definire delle operazioni tra cardinalità.
solo nel caso finito), con una serie di esercizi, vediamo
come si possano ugualmente definire delle operazioni tra cardinalità.
L'esercizio precedente permette di dare la seguente
Esercizio 7.2
Si provi che le operazioni appena definite, nel caso di insiemi finiti,
coincidono con le usuali operazioni tra numeri naturali.
Soluzione
Lasciamo come esercizio la dimostrazione del fatto che queste operazioni
verificano tutte le propruietà delle usuali operazioni tra numeri naturali.
L'assioma di buon ordinamento
Definizione 7.2
Sia
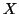
un insieme e sia
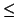
un ordinamento su
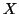
. Sia
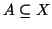
,
diremo che
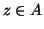
è un
minimo di
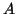
(in simboli
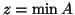
se
per ogni
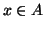
si ha che
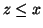
.
Definizione 7.3
Un ordinamento totale su un insieme
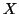
si dice un
buon ordinamento, e
in tal caso l'insieme ordinato
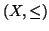
si dice
ben ordinato se ogni
sottinsieme non vuoto di
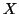
ha minimo.
Teorema 7.4 (buon ordinamento)
L'ordinamento dei numeri naturali è un buon ordinamento.
Dimostrazione.
Supponiamo che l'insieme
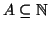 non abbia minimo e proviamo che
allora
non abbia minimo e proviamo che
allora 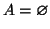 . Chiamiamo
. Chiamiamo 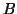 il suo complementare
(
il suo complementare
(
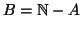 ) e dimostriamo per induzione che
) e dimostriamo per induzione che
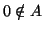 ,
altrimenti ne sarebbe il minimo, quindi
,
altrimenti ne sarebbe il minimo, quindi 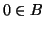 e pertanto
e pertanto
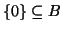 .
.
Supponiamo che
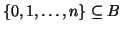 , allora
, allora
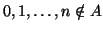 e
quindi
e
quindi 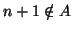 , altrimenti ne sarebbe il minimo, ma allora
, altrimenti ne sarebbe il minimo, ma allora 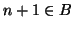 e
pertanto
e
pertanto
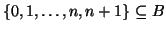 .
.
Ma allora 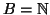 e quindi
e quindi 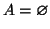 .
.

Il principio di induzione (seconda forma)
Teorema 7.5 (seconda forma dell'induzione)
Sia
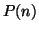
una famiglia di proposizioni indiciate su
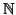
e si supponga che
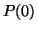 sia vera
sia vera
- per ogni
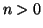
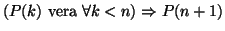
allora
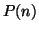
è vera per ogni
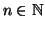
Dimostrazione.
Sia
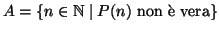 , e supponiamo per assurdo
che
, e supponiamo per assurdo
che
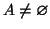 . Allora per la proprietà di buon ordinamento
. Allora per la proprietà di buon ordinamento  ha minimo
ha minimo  . Chiaramente
. Chiaramente 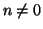 in quanto
in quanto
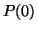 è vera. Inoltre se
è vera. Inoltre se 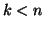 allora
allora 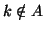 in quanto
in quanto 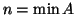 , ma
allora dalla (2) segue che
, ma
allora dalla (2) segue che 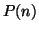 è vera e quindi
è vera e quindi 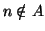 , contraddicendo
il fatto che
, contraddicendo
il fatto che 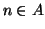 .
.

Osservazione 7.6
Si osservi che sia l'enunciato che la dimostrazione precedenti non usano il
fatto che si stia parlando di numeri naturali, ma soltanto che si sta
lavorando in un insieme bene ordinato. Quindi il principio di induzione in
questa forma è applicabile ad ogni insieme bene ordinato.
La divisione euclidea
Nel seguito denoteremo con 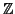 l'insieme dei numeri interi. Supporremo
nota la sua definizione e la definizione delle operazioni tra i suoi elementi.
Ci limitiamo a dire che gli interi e le operazioni tra interi possono essere
definiti a partire dai naturali e dalle operazioni tra naturali.
l'insieme dei numeri interi. Supporremo
nota la sua definizione e la definizione delle operazioni tra i suoi elementi.
Ci limitiamo a dire che gli interi e le operazioni tra interi possono essere
definiti a partire dai naturali e dalle operazioni tra naturali.
Dimostrazione. Esistenza. Supponiamo dapprima che
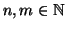 , ed usiamo il principio di
induzione nella seconda forma su
, ed usiamo il principio di
induzione nella seconda forma su 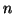 . Se
. Se 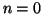 basta prendere
basta prendere 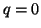 e
e 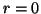 .
Supponiamo
.
Supponiamo 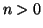 e che la tesi sia vera per ogni
e che la tesi sia vera per ogni 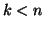 . Se
. Se 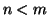 basta prendere
basta prendere
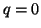 e
e 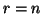 , altrimenti sia
, altrimenti sia 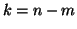 , dato che
, dato che 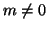
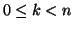 , quindi per
ipotesi di induzione esistono
, quindi per
ipotesi di induzione esistono
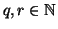 tali che
tali che
ma allora
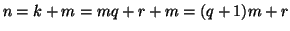 .
.
Supponiamo ora 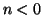 e
e 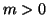 . Allora
. Allora 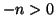 e quindi per il caso
precedente si ha che esistono
e quindi per il caso
precedente si ha che esistono
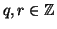 tali che
tali che 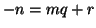 e
e
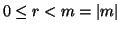 . E quindi
. E quindi 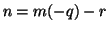 . Se
. Se 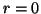 abbiamo finito, se invece
abbiamo finito, se invece
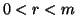 allora
allora
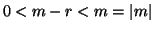 e
e
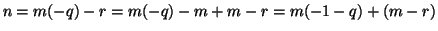 .
.
Sia infine 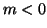 allora
allora 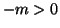 , quindi per i due casi precedenti
esistono
, quindi per i due casi precedenti
esistono
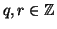 tali che
tali che
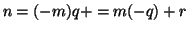 con
con
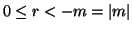 .
.
Unicità. Supponiamo che 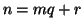 e
e 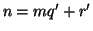 con
con 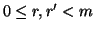 . Supponiamo
che
. Supponiamo
che 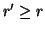 , allora
, allora 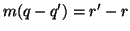 e
quindi passando ai moduli si ha
e
quindi passando ai moduli si ha
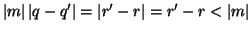 ,da cui
,da cui
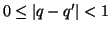 e quindi
e quindi
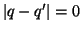 ovvero
ovvero 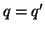 . Ma
allora da
. Ma
allora da 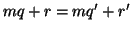 segue che anche
segue che anche 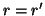 .
.

Osservazione 7.8
Si osservi che la dimostrazione del
teorema
di esistenza e unicità del quoziente e del resto della divisione euclidea di
due numeri naturali, permette di scrivere un algoritmo ricorsivo per il loro
calcolo:
che può essere tradotto nella scrittura di un programma ricorsivo per la
definizione di una funzione
DIVE che calcoli il quoziente e resto
della divisione euclidea tra due numeri:
Esercizio 7.5
Supponendo di avere un linguaggio di programmazione con un'istruzione
WHILE, tradurre la definizione della funzione
DIVE in una
funzione non ricorsiva (induttiva).
Soluzione


Next: Lezione 8 (21 marzo
Up: Matematica Discreta
Previous: Lezione 6 (14 marzo
Luminati Domenico
2002-06-07
![]() solo nel caso finito), con una serie di esercizi, vediamo
come si possano ugualmente definire delle operazioni tra cardinalità.
solo nel caso finito), con una serie di esercizi, vediamo
come si possano ugualmente definire delle operazioni tra cardinalità.
![]() non abbia minimo e proviamo che
allora
non abbia minimo e proviamo che
allora ![]() . Chiamiamo
. Chiamiamo ![]() il suo complementare
(
il suo complementare
(
![]() ) e dimostriamo per induzione che
) e dimostriamo per induzione che
![]() , allora
, allora
![]() e
quindi
e
quindi ![]() , altrimenti ne sarebbe il minimo, ma allora
, altrimenti ne sarebbe il minimo, ma allora ![]() e
pertanto
e
pertanto
![]() .
.
![]() e quindi
e quindi ![]() .
.
![]()
![]() , e supponiamo per assurdo
che
, e supponiamo per assurdo
che
![]() . Allora per la proprietà di buon ordinamento
. Allora per la proprietà di buon ordinamento ![]() ha minimo
ha minimo ![]() . Chiaramente
. Chiaramente ![]() in quanto
in quanto
![]() è vera. Inoltre se
è vera. Inoltre se ![]() allora
allora ![]() in quanto
in quanto ![]() , ma
allora dalla (2) segue che
, ma
allora dalla (2) segue che ![]() è vera e quindi
è vera e quindi ![]() , contraddicendo
il fatto che
, contraddicendo
il fatto che ![]() .
.
![]()
![]() , ed usiamo il principio di
induzione nella seconda forma su
, ed usiamo il principio di
induzione nella seconda forma su ![]() . Se
. Se ![]() basta prendere
basta prendere ![]() e
e ![]() .
Supponiamo
.
Supponiamo ![]() e che la tesi sia vera per ogni
e che la tesi sia vera per ogni ![]() . Se
. Se ![]() basta prendere
basta prendere
![]() e
e ![]() , altrimenti sia
, altrimenti sia ![]() , dato che
, dato che ![]()
![]() , quindi per
ipotesi di induzione esistono
, quindi per
ipotesi di induzione esistono
![]() tali che
tali che
![]() e
e ![]() . Allora
. Allora ![]() e quindi per il caso
precedente si ha che esistono
e quindi per il caso
precedente si ha che esistono
![]() tali che
tali che ![]() e
e
![]() . E quindi
. E quindi ![]() . Se
. Se ![]() abbiamo finito, se invece
abbiamo finito, se invece
![]() allora
allora
![]() e
e
![]() .
.
![]() allora
allora ![]() , quindi per i due casi precedenti
esistono
, quindi per i due casi precedenti
esistono
![]() tali che
tali che
![]() con
con
![]() .
.
![]() e
e ![]() con
con ![]() . Supponiamo
che
. Supponiamo
che ![]() , allora
, allora ![]() e
quindi passando ai moduli si ha
e
quindi passando ai moduli si ha
![]() ,da cui
,da cui
![]() e quindi
e quindi
![]() ovvero
ovvero ![]() . Ma
allora da
. Ma
allora da ![]() segue che anche
segue che anche ![]() .
.
![]()

