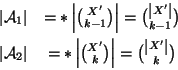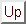

Next: Lezione 9 (26 marzo
Up: Matematica Discreta
Previous: Lezione 7 (19 marzo
Subsections
Definizione 8.1
Sia
. Diremo che
è
rappresentabile in base
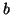
se esistono numeri
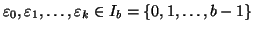
tali
che
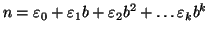
.
Osservazione 8.2
Si osservi che nessun numero è rappresentabile in base
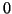
(dato che
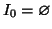
) e che l'unico numero rappresentabile in base
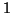
è lo
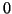
. In
questo caso infatti la condizione (
2) implica che ogni
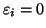
.
Teorema 8.4 (rappresentazione dei naturali in base arbitraria)
Sia
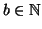
,
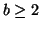
. Allora ogni
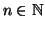
è rappresentabile in modo unico in
base
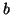
.
Ossia esiste esiste una
successione
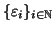
come nell'
osservazione
precedente e se
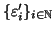
è un'altra tale successione, allora
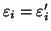
per ogni
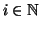
.
Dimostrazione.
Dimostriamo l'esistenza per induzione su 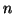 . Se
. Se 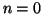 basta prendere
basta prendere
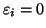 per ogni
per ogni
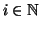 . Supponiamo ora
. Supponiamo ora 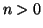 e che la tesi sia
vera per ogni
e che la tesi sia
vera per ogni 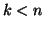 . Siano
. Siano 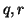 tali che
tali che 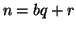 con
con 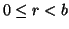 .
Dato che
.
Dato che 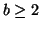 si ha che
si ha che
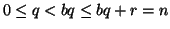 e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
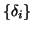 , costituita di interi tali che
, costituita di interi tali che
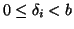 per
ogni
per
ogni 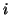 e tale che
e tale che
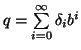 . Ma
allora
. Ma
allora
dove si è posto
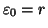 e
e
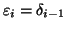 per ogni
per ogni 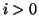 . La
successione
. La
successione
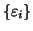 è definitivamente nulla, dato che lo è
è definitivamente nulla, dato che lo è
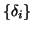 ed inoltre
ed inoltre
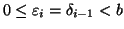 per ogni
per ogni 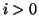 e
e
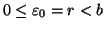 .
.
Dimostriamo ora l'unicità. Procediamo per induzione su 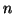 . Se
. Se
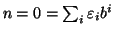 allora ogni addendo della somma essendo
non negativo, deve essere nullo e quindi
allora ogni addendo della somma essendo
non negativo, deve essere nullo e quindi
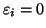 per ogni
per ogni 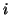 .
.
Supponiamo ora 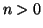 e che l'espressione in base
e che l'espressione in base 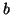 sia unica per
tutti i numeri
sia unica per
tutti i numeri 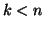 . Sia
. Sia 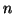 tale che
tale che
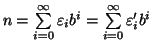 . Allora possiamo scrivere
. Allora possiamo scrivere
ma per l'unicità della divisione euclidea si ha che
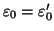 e
e
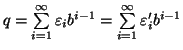 . Come prima
. Come prima 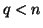 e quindi per ipotesi di induzione si ha anche che
e quindi per ipotesi di induzione si ha anche che
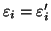 per ogni
per ogni 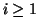 .
.

Osservazione 8.5
Anche in questo caso la dimostrazione del
teorema di rappresentazione in base
assegnata dei naturali, permette di scrivere un algoritmo ricorsivo per il
calcolo della stringa degli
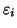
algoritmo che può essere tradotto in un programma ricorsivo per la definizione
di una funzione
B_RAPP che calcoli la rappresentazione di un numero in
base fissata.
Il coefficiente binomiale
Osservazione 8.7
È immediato verificare che
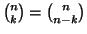
.
 -sottinsiemi
-sottinsiemi
Definizione 8.8
Sia
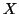
un insieme e
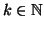
, un sottinsieme
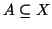
sarà detto un
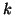 -sottinsieme
-sottinsieme se
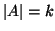
. Denoteremo con
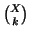
l'insieme dei
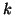
-sottinsiemi di
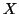
. I
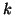
-sottinsiemi sono anche chiamati
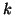 -combinazioni semplici
-combinazioni semplici.
Dimostrazione.
Procediamo per induzione su
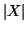 . Se
. Se
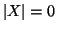 allora
allora 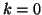 e
e
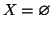 . Ma allora
. Ma allora
Supponiamo ora che
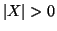 . Se
. Se
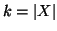 , allora
, allora
 e quindi
e quindi
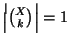 . D'altra parte
anche
. D'altra parte
anche
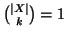 . ANche il caso
. ANche il caso 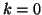 è facile. Supponiamo
allora
è facile. Supponiamo
allora
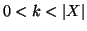 . Fissiamo
. Fissiamo 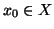 un elemento e poniamo
un elemento e poniamo
chiaramente si ha
da cui
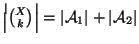 )cfr
esercizio4.2). Posto
)cfr
esercizio4.2). Posto 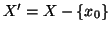 si ha che
si ha che
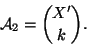 |
(7) |
inoltre la funzione
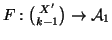 definita da
definita da
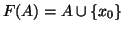 è una bigezione e quindi, dato che
è una bigezione e quindi, dato che
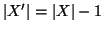 , per ipotesi di induzione si ha
, per ipotesi di induzione si ha
Ma allora, usando il risultato dell'esercizio 8.1

Una sestina al Superenalotto, è un sottinsieme di 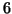 elementi dell'insieme
dei numeri naturali da
elementi dell'insieme
dei numeri naturali da 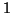 a
a 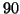 , quindi, per la proposizione 8.9
il numero di sestine possibili è dato da:
, quindi, per la proposizione 8.9
il numero di sestine possibili è dato da:
Pertanto, la probabilità di vincere giocando una sestina è pari a
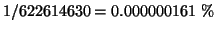 di vincere giocando una sestina. Se quindi il
gioco fosse equo, la puntata su una giocata dovrebbe essere pagata
di vincere giocando una sestina. Se quindi il
gioco fosse equo, la puntata su una giocata dovrebbe essere pagata 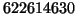 volte la posta. Dato che la puntata su una sestina costa
volte la posta. Dato che la puntata su una sestina costa 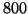 L., mi
aspetterei, in caso di successo, un premio di
L., mi
aspetterei, in caso di successo, un premio di
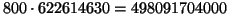 L.
L.
Un montepremi così alto non si è ancora visto!


Next: Lezione 9 (26 marzo
Up: Matematica Discreta
Previous: Lezione 7 (19 marzo
Luminati Domenico
2002-06-07
![]() . Se
. Se ![]() basta prendere
basta prendere
![]() per ogni
per ogni
![]() . Supponiamo ora
. Supponiamo ora ![]() e che la tesi sia
vera per ogni
e che la tesi sia
vera per ogni ![]() . Siano
. Siano ![]() tali che
tali che ![]() con
con ![]() .
Dato che
.
Dato che ![]() si ha che
si ha che
![]() e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
e quindi per ipotesi
di induzione esiste una successione definitivamente nulla
![]() , costituita di interi tali che
, costituita di interi tali che
![]() per
ogni
per
ogni ![]() e tale che
e tale che
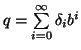 . Ma
allora
. Ma
allora
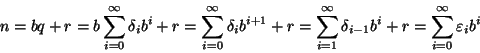
![]() . Se
. Se
![]() allora ogni addendo della somma essendo
non negativo, deve essere nullo e quindi
allora ogni addendo della somma essendo
non negativo, deve essere nullo e quindi
![]() per ogni
per ogni ![]() .
.
![]() e che l'espressione in base
e che l'espressione in base ![]() sia unica per
tutti i numeri
sia unica per
tutti i numeri ![]() . Sia
. Sia ![]() tale che
tale che
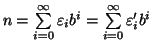 . Allora possiamo scrivere
. Allora possiamo scrivere
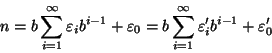
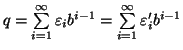 . Come prima
. Come prima 

![]() . Se
. Se
![]() allora
allora ![]() e
e
![]() . Ma allora
. Ma allora